题目内容
7.如图(1),PT与⊙O1相切于点T,PB与⊙O1相交于A、B两点,可证明△PTA∽△PBT,从而有PT2=PA•PB.请应用以上结论解决下列问题:如图(2),PAB、PCD分别与⊙O2相交于A、B、C、D四点,已知PA=2,PB=7,PC=3,则CD=$\frac{5}{3}$.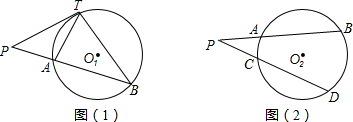
分析 如图2中,过点P作⊙O的切线PT,切点是T,根据PT2=PA•PB=PC•PD,求出PD即可解决问题.
解答 解:如图2中,过点P作⊙O的切线PT,切点是T.
∵PT2=PA•PB=PC•PD,
∵PA=2,PB=7,PC=3,
∴2×7=3×PD,
∴PD=$\frac{14}{3}$
∴CD=PD-PC=$\frac{14}{3}$-3=$\frac{5}{3}$.
点评 本题考查相似三角形的判定和性质、切线的性质等知识,解题的关键是理解题意,学会利用新知解决未知,属于中考常考题型.

练习册系列答案
相关题目
18.下列事件属于必然事件的是( )
| A. | 姚明罚球线上投篮,投进篮筐 | |
| B. | 某种彩票的中奖率为$\frac{1}{100}$,购买100张彩票一定中奖 | |
| C. | 掷一次骰子,向上一面的点数是6 | |
| D. | 367人中至少有两人的生日在同一天 |
15.在Rt△ABC中,∠C=90°,sinA=$\frac{3}{5}$,BC=6,则AB=( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |






 如图,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长为( )
如图,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长为( ) 如图,下面的几何体由三个大小相同的小立方块组成,则它的左视图是( )
如图,下面的几何体由三个大小相同的小立方块组成,则它的左视图是( )



 如图,分别以边长等于1的正方形的四边为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$π-1.
如图,分别以边长等于1的正方形的四边为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$π-1.