题目内容
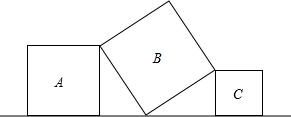如图，将三个大小不同的正方形如图放置，顶点处两两相接，若正方形A的边长为4，C的边长为3，则B的边长为考点：全等三角形的判定与性质,勾股定理
专题：
分析：易证∠FDE=∠GEH，即可证明△DEF≌△EGH，可得EF的长，根据勾股定理即可求得DE的长，即可解题．
解答：解：
∵∠DEF+∠GEH=90°，∠DEF+∠FDE=90°，
∴∠FDE=∠GEH，
∵在△DEF和△EGH中，
，
∴△DEF≌△EGH，（AAS）
∴EF=GH=3，
∴DE=
=5，
故答案为5．
∵∠DEF+∠GEH=90°，∠DEF+∠FDE=90°，
∴∠FDE=∠GEH，
∵在△DEF和△EGH中，
|
∴△DEF≌△EGH，（AAS）
∴EF=GH=3，
∴DE=
| EF2+DF2 |
故答案为5．
点评：本题考查了全等三角形的判定和全等三角形对应边相等的性质，考查了勾股定理的运用，本题中求证△DEF≌△EGH是解题的关键．
练习册系列答案
相关题目
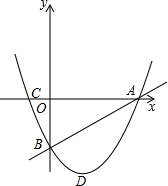如图，抛物线y1=x2+bx-c经过直线y2=x-3与坐标轴的两个交点A、B，此抛物线与x轴的另一个交点为C，抛物线顶点为D．二次函数y=x2+x-6的图象与x轴两个交点的坐标分别为（ ）
| A、（2，0），（-3，0） |
| B、（-2，0），（3，0） |
| C、（2，0），（3，0） |
| D、（-2，0），（-3，0） |