题目内容
6.一个蓄水池有甲、乙两个进水管和一个丙排水管,单独开甲管6小时可注满水池;单独开乙管8小时可注满水池,单独开丙管9小时可将满池水排空,若先将甲、乙管同时开放2小时,然后打开丙管,问打开丙管后几小时可注满水池?分析 设打开丙管后x小时可注满水池.等量关系为:甲注水量+乙注水量-丙排水量=1. 据此列出方程并解答.
解答 解:设打开丙管后x小时可注满水池,
由题意得,($\frac{1}{6}$+$\frac{1}{8}$)(x+2)-$\frac{1}{9}x$=1,
解这个方程,$\frac{7}{24}$(x+2)-$\frac{x}{9}$=1,
21x+42-8x=72,
13x=30,
解得x=$\frac{30}{13}$.
答:打开丙管后$\frac{30}{13}$小时可注满水池.
点评 本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
1.某企业为了增收节支,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
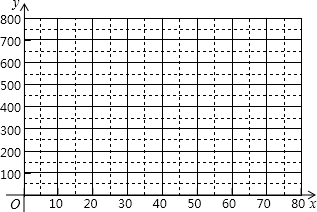
(1)把上表中x、y的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点,猜想y与x之间的函数关系式,并求出函数关系式;
(2)市物价部门规定,销售部门规定该工艺品单价不得超过48元,要想每天获得8750元利润,单价应定为多少元?(利润=销售总价-成本总价 )
| 销售单价x元/件 | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y件 | … | 500 | 400 | 300 | 200 | 100 | … |

(1)把上表中x、y的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点,猜想y与x之间的函数关系式,并求出函数关系式;
(2)市物价部门规定,销售部门规定该工艺品单价不得超过48元,要想每天获得8750元利润,单价应定为多少元?(利润=销售总价-成本总价 )
 如图,△ABC中,AB=AC,点E是AC上一点,ED⊥BC于点D,DE的延长线交BA的延长线于点F.求证:△AEF是等腰三角形.
如图,△ABC中,AB=AC,点E是AC上一点,ED⊥BC于点D,DE的延长线交BA的延长线于点F.求证:△AEF是等腰三角形.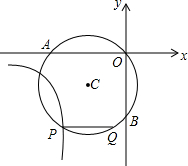 如图,过原点O的⊙C与两坐标轴分别交于点A(-4,0)、B(0,-3),在第三象限的⊙C上有一点P,过点P作弦PQ∥x轴,且PQ=3,已知双曲线y=$\frac{k}{x}$过点P,则k的值是$\frac{49}{4}$.
如图,过原点O的⊙C与两坐标轴分别交于点A(-4,0)、B(0,-3),在第三象限的⊙C上有一点P,过点P作弦PQ∥x轴,且PQ=3,已知双曲线y=$\frac{k}{x}$过点P,则k的值是$\frac{49}{4}$.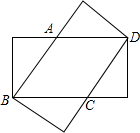 如图,四边形EBGD和四边形BFDH是两个全等的矩形,其中ED、BH交于点A,BG、FD交于点C.
如图,四边形EBGD和四边形BFDH是两个全等的矩形,其中ED、BH交于点A,BG、FD交于点C.