题目内容
7.吸烟有害健康,为配合“戒烟”运动,某校组织同学们在某社区开展了“你支持哪种戒烟方式”的随机问卷调查,并调查结果绘制成两幅不完整的统计图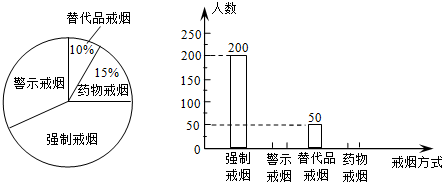
根据统计图解答下列问题:
(Ⅰ)同学们一共调查了多少人?
(Ⅱ)将条形统计图补充完整.
(Ⅲ)若该社区有8000人,请你估计大约会有多少人不支持“强制戒烟”这种方式?
分析 (1)根据替代品戒烟50人占总体的10%,即可求得总人数;
(2)根据求得的总人数,结合扇形统计图可以求得药物戒烟的人数,从而求得警示戒烟的人数,再根据各部分的人数除以总人数,即可求得各部分所占的百分比;
(3)根据利用总人数8000乘以不支持强制戒烟的人数所占的比例即可求得.
解答 解:(1)50÷10%=500(人).
故一共调查了500人.
(2)由(1)可知,总人数是500人.
药物戒烟:500×15%=75(人);
警示戒烟:500-200-50-75=175(人);175÷500=35%;
强制戒烟:200÷500=40%.
完整的统计图如图所示:
(3)8000×(1-40%)=4800(人),
答:大约有4800人不支持“警示戒烟”这种方式.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
18.tan30°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
2.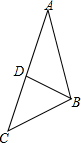 如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③AD•BC=AB•BD;④AB•BC=AC•BD.其中单独能够判定△ABC∽△ADB的个数是( )
如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③AD•BC=AB•BD;④AB•BC=AC•BD.其中单独能够判定△ABC∽△ADB的个数是( )
 如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③AD•BC=AB•BD;④AB•BC=AC•BD.其中单独能够判定△ABC∽△ADB的个数是( )
如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③AD•BC=AB•BD;④AB•BC=AC•BD.其中单独能够判定△ABC∽△ADB的个数是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
12.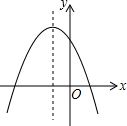 已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在( )
已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在( )
 已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在( )
已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
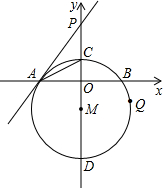 如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若⊙M的半径为5,点A的坐标为(-4,0),
如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若⊙M的半径为5,点A的坐标为(-4,0),