题目内容
2.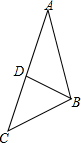 如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③AD•BC=AB•BD;④AB•BC=AC•BD.其中单独能够判定△ABC∽△ADB的个数是( )
如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③AD•BC=AB•BD;④AB•BC=AC•BD.其中单独能够判定△ABC∽△ADB的个数是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 根据有两个角对应相等的三角形相似,可判断①,根据两边对应成比例且夹角相等的两个三角形相似,可判断断②③④.
解答 解:①∵∠ABD=∠ACB,∠A=∠A,∴△ABC∽△ADB;
②∵AB2=AD•AC,∴$\frac{AC}{AB}$=$\frac{AB}{AD}$,∠A=∠A,△ABC∽△ADB;
③∵AD•BC=AB•BD,∴$\frac{AB}{AD}$=$\frac{BC}{BD}$,∠A=∠A,△ABC与△ADB不相似;
④∵AB•BC=AC•BD,∴$\frac{AC}{AB}$=$\frac{BC}{BD}$,∠A=∠A,△ABC与△ADB不相似;
故选:A.
点评 本题考查了相似三角形的判定,利用了有两个角对应相等的三角形相似,两边对应成比例且夹角相等的两个三角形相似.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目

 吉福市实行了生活用电按三个档次收费方案,下图是每户人家每月用电费y(元)与用电量x(度)间的关系
吉福市实行了生活用电按三个档次收费方案,下图是每户人家每月用电费y(元)与用电量x(度)间的关系
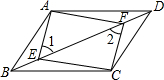 如图,已知E,F是平行四边形ABCD对角线BD上的点,∠1=∠2.
如图,已知E,F是平行四边形ABCD对角线BD上的点,∠1=∠2.