题目内容
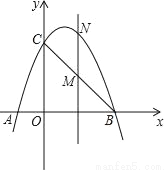
如图,已知抛物线经过点A(﹣1,0),B(3,0),C(0,3)三点.
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点m,使△BNC的面积最大?若存在,求m的值和△BNC的面积;若不存在,说明理由.
练习册系列答案
相关题目
题目内容
如图,已知抛物线经过点A(﹣1,0),B(3,0),C(0,3)三点.
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点m,使△BNC的面积最大?若存在,求m的值和△BNC的面积;若不存在,说明理由.
