题目内容
16.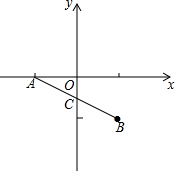 如图,已知A(-2,0),B(2,-2),线段AB交y轴于点C.
如图,已知A(-2,0),B(2,-2),线段AB交y轴于点C.(1)求C点坐标.
(2)若D(6,0),动点P从D点开始在x轴上以每秒3个单位向左运动,同时,动点Q从C点开始在y轴上以每秒1个单位向下运动.问经过多少秒,S△APC=S△AOQ?
分析 (1)利用A,B点坐标,结合三角形中位线定理得出CO的长,进而得出C点坐标;
(2)利用P点在A点右侧或,P点在A点左侧分别得出符合题意的答案.
解答 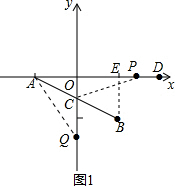 解:(1)如图1所示:过点B作BE⊥x轴于点E,
解:(1)如图1所示:过点B作BE⊥x轴于点E,
∵A(-2,0),B(2,-2),
∴AO=OE=2,BE=2,
可得;CO∥BE,
则CO=$\frac{1}{2}$BE=1,
故C(0,-1);
(2)如图1所示:设t秒时,P点在A点右侧,S△APC=S△AOQ,
则S△APC=$\frac{1}{2}$×AP×CO=$\frac{1}{2}$×(8-3t)×1=4-$\frac{3}{2}$t,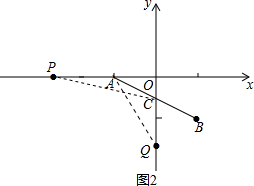
S△AOQ=$\frac{1}{2}$×AO×QO=$\frac{1}{2}$×2×(1+t)=1+t,
则4-$\frac{3}{2}$t=1+t,
解得:t=$\frac{6}{5}$;
如图2所示:设t秒时,P点在A点左侧,S△APC=S△AOQ,
则S△APC=$\frac{1}{2}$×AP×CO=$\frac{1}{2}$×(3t-8)×1=$\frac{3}{2}$t-4,
S△AOQ=$\frac{1}{2}$×AO×QO=$\frac{1}{2}$×2×(1+t)=1+t,
则$\frac{3}{2}$t-4=1+t,
解得:t=10,
综上所述:t=$\frac{6}{5}$或10秒时,S△APC=S△AOQ.
点评 此题主要考查了坐标与图形的性质以及三角形面积求法等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
6. 记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )
记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )
 记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )
记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )| A. | $\frac{2013×2012}{4}$ | B. | $\frac{2013×2012}{2}$ | C. | $\frac{503×2013}{2}$ | D. | $\frac{2012×2011}{4}$ |
7.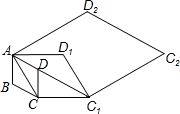 如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
 如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )| A. | $\frac{\sqrt{3}}{2}$×3n | B. | $\frac{\sqrt{3}}{2}$×3n+1 | C. | $\frac{\sqrt{3}}{2}$×3n-1 | D. | $\frac{\sqrt{3}}{2}$×32n-1 |
4.小美将某服饰店的促销活动内容告诉小明后,小明假设某一商品的定价为x元,并列出关系式为0.3(2x-100)<1000,则下列何者可能是小美告诉小明的内容?( )
| A. | 买两件等值的商品可减100元,再打3折,最后不到1000元 | |
| B. | 买两件等值的商品可减100元,再打7折,最后不到1000元 | |
| C. | 买两件等值的商品可打3折,再减100元,最后不到1000元 | |
| D. | 买两件等值的商品可打7折,再减100元,最后不到1000元 |
1.等边三角形的边心距、半径、边长之比为( )
| A. | 1:$\sqrt{3}$:2 | B. | 1:2:$\sqrt{3}$ | C. | 1:2$\sqrt{3}$:2 | D. | 1:2:2$\sqrt{3}$ |
 如图,在周长为12cm的矩形铁板上剪去一个等边三角形(这个三角形的一边是矩形的宽),则矩形的宽为$\frac{12(4-\sqrt{3})}{13}$cm时,剩下铁板的面积最大.
如图,在周长为12cm的矩形铁板上剪去一个等边三角形(这个三角形的一边是矩形的宽),则矩形的宽为$\frac{12(4-\sqrt{3})}{13}$cm时,剩下铁板的面积最大.