题目内容
14. 如图,P、Q是反比例函数图象上两点,且关于原点对称,QE⊥x轴,矩形PEQF的面积是3,则反比例函数的表达式为y=-$\frac{3x}{4}$.
如图,P、Q是反比例函数图象上两点,且关于原点对称,QE⊥x轴,矩形PEQF的面积是3,则反比例函数的表达式为y=-$\frac{3x}{4}$.
分析 设反比例函数的表达式为y=$\frac{k}{x}$,由于P、Q是反比例函数图象上两点,且关于原点对称,QE⊥x轴,于是得到|k|=$\frac{1}{4}$S四边形PEQF=$\frac{3}{4}$,即可得到结果.
解答 解:设反比例函数的表达式为y=$\frac{k}{x}$,
∵P、Q是反比例函数图象上两点,且关于原点对称,QE⊥x轴,
∴|k|=$\frac{1}{4}$S四边形PEQF=$\frac{3}{4}$,
∵反比例函数的图象在第二,四象限,
∴k=-$\frac{3}{4}$,
∴反比例函数的表达式为y=-$\frac{3x}{4}$,
故答案为:y=-$\frac{3x}{4}$.
点评 本题考查了反比例函数系数k的几何意义,反比例函数的性质,熟练掌握反比例函数系数k的几何意义是解题的关键.

练习册系列答案
相关题目
4.方程x2-7x+12=0的解为( )
| A. | 3或4 | B. | -3或-4 | C. | -3或4 | D. | 3或-4 |
6. 记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )
记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )
 记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )
记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )| A. | $\frac{2013×2012}{4}$ | B. | $\frac{2013×2012}{2}$ | C. | $\frac{503×2013}{2}$ | D. | $\frac{2012×2011}{4}$ |
4.小美将某服饰店的促销活动内容告诉小明后,小明假设某一商品的定价为x元,并列出关系式为0.3(2x-100)<1000,则下列何者可能是小美告诉小明的内容?( )
| A. | 买两件等值的商品可减100元,再打3折,最后不到1000元 | |
| B. | 买两件等值的商品可减100元,再打7折,最后不到1000元 | |
| C. | 买两件等值的商品可打3折,再减100元,最后不到1000元 | |
| D. | 买两件等值的商品可打7折,再减100元,最后不到1000元 |
 如图,已知:A、F、C、D四点在一条直线上,AF=CD,BC=EF,且AB=DE. 请说明△ABC≌△DEF.
如图,已知:A、F、C、D四点在一条直线上,AF=CD,BC=EF,且AB=DE. 请说明△ABC≌△DEF.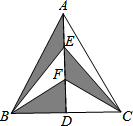 如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的三等分点,若△ABC的面积为12cm2,则图中的阴影面积是6cm2.
如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的三等分点,若△ABC的面积为12cm2,则图中的阴影面积是6cm2. 如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.则这组数据的中位数是30.
如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.则这组数据的中位数是30.