题目内容
19.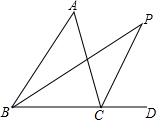 如图,△ABC的内角平分线BP和外角平分线CP交于点P,∠A=52°,则∠P=26°.
如图,△ABC的内角平分线BP和外角平分线CP交于点P,∠A=52°,则∠P=26°.
分析 根据三角形的内角和定理得出∠A+∠ABC+∠ACB=180°,∠P+∠PBC+∠PCB=180°,再由角平分线的定义得出∠ABC=2∠PBC,∠ACD=2∠PCA,整理即可得出∠P的度数.
解答 解:∵BP,CP分别平分∠ABC,∠ACD,
∴∠ABC=2∠PBC,∠ACD=2∠PCA,
∵∠A+∠ABC+∠ACB=180°,∠P+∠PBC+∠PCB=180°,
∴∠A+2∠PBC+∠ACB=180°,
∠P+∠PBC+∠PCA+∠ACB=180°,
∴∠A+∠PBC=∠P+∠PCA,
∵∠PCA=$\frac{180°-∠ACB}{2}$,
∴∠A+$\frac{1}{2}$∠ABC=∠P+90-$\frac{1}{2}$∠BCA,
∴∠P=$\frac{1}{2}$(∠BCA+∠ABC)+∠A-90°,
∴∠P=$\frac{1}{2}$(180°-∠A)+∠A-90°,
∴∠P=$\frac{1}{2}$∠A,
∵∠A=52°,
∴∠P=26°,
故答案为26°.
点评 本题考查了三角形的内角和定理,以及角平分线的定义,根据角平分线的定义把角进行转化是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.如图所示,下列图案中是轴对称图形的共有( )


| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
7.下列交换加数位置的变形中,正确的是( )
| A. | 1-4+5-4=1-4+4-5 | |
| B. | 4.5-1.7-2.5+1.8=4.5-2.5+1.8-1.7 | |
| C. | 1-2+3-4=2-1+4-3 | |
| D. | -$\frac{1}{3}$+$\frac{3}{4}$-$\frac{1}{6}$-$\frac{1}{4}$=$\frac{1}{4}$+$\frac{3}{4}$-$\frac{1}{3}$-$\frac{1}{6}$ |
14.已知y=ax2(a≠0)的图象不经过第四象限,图象上有A(-1,y1),B(-$\sqrt{2}$,y2),C(2,y3)三点,则y1、y2、y3的大小关系为( )
| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y2>y1>y3 | D. | y3>y1>y2 |
 如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的从正面看的图和从左面看的图:
如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的从正面看的图和从左面看的图: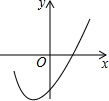 如图二次函数y=ax2+bx+c的部分图象及顶点坐标(-1,-3.2),由图象可知关于x的方程ax2+bx+c=0的两根x1=1.3,x2=-3.3.
如图二次函数y=ax2+bx+c的部分图象及顶点坐标(-1,-3.2),由图象可知关于x的方程ax2+bx+c=0的两根x1=1.3,x2=-3.3.