题目内容
12.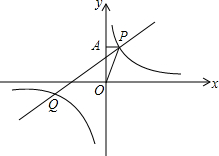 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+4的图象交于P,Q两点,并且P点的纵坐标为6,直线y=ax+4交y轴于点A,且S△POA=4.
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+4的图象交于P,Q两点,并且P点的纵坐标为6,直线y=ax+4交y轴于点A,且S△POA=4.(1)求两函数解析式;
(2)求P,Q点坐标.
分析 (1)首先根据点A的坐标,结合S△POA=4求得点P的横坐标,再根据点P的坐标求得反比例函数和一次函数的解析式;
(2)联立方程,解方程即可求得.
解答 解:(1)∵直线y=ax+4交y轴于点A,
∴A(0,4),
∴OA=4,
∵S△POA=4.
∴$\frac{1}{2}$OA•|xP|=4,解得xP=2,
∵P点的纵坐标为6,
∴P(2,6),
∵反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+4的图象交于P,Q两点,
∴6=$\frac{k}{2}$,6=2a+4,解得k=12,a=1,
∴反比例函数为y=$\frac{12}{x}$,一次函数y=x+4;
(2)解$\left\{\begin{array}{l}{y=\frac{12}{x}}\\{y=x+4}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$或$\left\{\begin{array}{l}{x=-6}\\{y=-2}\end{array}\right.$,
∴P,Q点坐标分别为(2,6),(-6,-2).
点评 本题考查了反比例函数与一次函数的交点问题.根据题意求得P点的坐标是解题的关键.

练习册系列答案
相关题目
2.一只蚂蚁从数轴上A点出发爬了6个单位长度到了表示1的点,则点A所表示的数是( )
| A. | 7 | B. | -5 | C. | 7或-5 | D. | 5或-7 |
7.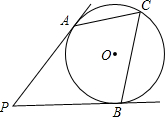 如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.
如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.
 如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.
如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.| A. | 26° | B. | 62° | C. | 65° | D. | 52° |
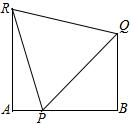 设在一条小巷内,∠A=∠B=90°,一个梯子的底脚位于点P处,当该梯子顶端靠在小巷一侧的墙上点Q时,梯子的倾斜角为45°,当顶端靠在小巷的另一侧墙上时,其顶端R离开地面高度为4米,且此时梯子的倾斜角为75°.
设在一条小巷内,∠A=∠B=90°,一个梯子的底脚位于点P处,当该梯子顶端靠在小巷一侧的墙上点Q时,梯子的倾斜角为45°,当顶端靠在小巷的另一侧墙上时,其顶端R离开地面高度为4米,且此时梯子的倾斜角为75°. 如图所示,A是直线上的一个点,请你在A点的右侧每隔1厘米取一个点,共取三个点,那么
如图所示,A是直线上的一个点,请你在A点的右侧每隔1厘米取一个点,共取三个点,那么