题目内容
13.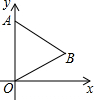 如图,已知等边三角形OAB的顶点O(0,0),A(0,3),将该三角形绕点O顺时针旋转,每次旋转60°,则旋转2017次后,顶点B的坐标为($\frac{3\sqrt{3}}{2}$,-$\frac{3}{2}$).
如图,已知等边三角形OAB的顶点O(0,0),A(0,3),将该三角形绕点O顺时针旋转,每次旋转60°,则旋转2017次后,顶点B的坐标为($\frac{3\sqrt{3}}{2}$,-$\frac{3}{2}$).
分析 由点B的旋转周期为6知点B旋转2017次后的坐标与旋转1次后的坐标相同,再结合图形解直角三角形得出点B旋转1次后的坐标即可得.
解答 解:由题意知点B旋转$\frac{360°}{60°}$=6次后与点B重合,即点B的旋转周期为6,
∵2017÷6=336…1,
∴点B旋转2017次后的坐标与旋转1次后的坐标相同,
如图,OB绕点O顺时针旋转60°得到OB1,过点B1作B1C⊥x轴,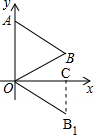
∵△OAB为等边三角形,且A(0,3),
∴OA=OB=OB1=3,∠AOB=60°,
∴∠BOC=∠B1OC=30°,
则B1C=OB1sin∠B1OC=3×$\frac{1}{2}$=$\frac{3}{2}$,OC=OB1cos∠B1OC=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,
∴旋转2017次后,顶点B的坐标为($\frac{3\sqrt{3}}{2}$,-$\frac{3}{2}$),
故答案为:($\frac{3\sqrt{3}}{2}$,-$\frac{3}{2}$).
点评 本题主要考查坐标与图形的变化-旋转,根据题意得出点B的旋转周期为6及旋转的性质、解直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC. 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{6}{x}$的图象相交于A(2,m),B(n,1)两点,连接OA,OB,则△OAB的面积为( )
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{6}{x}$的图象相交于A(2,m),B(n,1)两点,连接OA,OB,则△OAB的面积为( )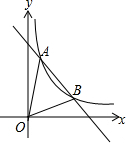 如图,已知反比例函数y=kx-1(k>0)的图象与一次函数图象y=-x+4交于a、b两点,点a的纵坐标为3.
如图,已知反比例函数y=kx-1(k>0)的图象与一次函数图象y=-x+4交于a、b两点,点a的纵坐标为3.