题目内容
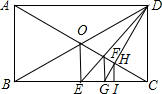 如图,在矩形ABCD中,对角线AC、BD相交于点O.
如图,在矩形ABCD中,对角线AC、BD相交于点O.(1)过点O作OE⊥BC于E点,连接DE交OC于F点,作FG⊥BC于G点,则△ABC与△FGC是位似三角形吗?若是,请说出位似中心,并求出位似比;若不是,请说明理由.
(2)同(1)的操作步骤,试确定
| CI |
| BC |
考点:位似变换
专题:
分析:(1)利用位似图形的性质得出位似中心进而利用平行线分线段成比例定理求出即可;
(2)利用平行线分线段成比例定理求出即可.
(2)利用平行线分线段成比例定理求出即可.
解答:解:(1)△ABC与△FGC是位似三角形,C是位似中心;
∵在矩形ABCD中,对角线AC、BD相交于点O,OE⊥BC,
∴
=
=
,
由题意可得:EO∥FG∥HI,
则
=
,
设EG=y,则GC=2y,
故
=
=
=
,
即位似比为:
;
(2)由(1)得
=
,
故
=
,
则IC=
y,
故
=
=
.
∵在矩形ABCD中,对角线AC、BD相交于点O,OE⊥BC,
∴
| EO |
| AB |
| EO |
| CD |
| 1 |
| 2 |
由题意可得:EO∥FG∥HI,
则
| EG |
| GC |
| 1 |
| 2 |
设EG=y,则GC=2y,
故
| EG |
| EC |
| FG |
| CD |
| FG |
| AB |
| 1 |
| 3 |
即位似比为:
| 1 |
| 3 |
(2)由(1)得
| GI |
| GC |
| 1 |
| 3 |
故
| GI |
| IC |
| 1 |
| 2 |
则IC=
| 4 |
| 3 |
故
| CI |
| BC |
| ||
| 6y |
| 2 |
| 9 |
点评:此题主要考查了位似图形的性质以及平行线分线段成比例定理,利用未知数表示各线段长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
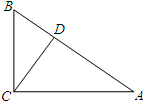 如图,在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=1.8.求AD的长.
如图,在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=1.8.求AD的长.