题目内容
一个等腰三角形的周长是62,其中第一条边的长是第二条边的
加10,求这个三角形的边长.
| 2 |
| 3 |
考点:等腰三角形的性质,三角形三边关系
专题:
分析:设第一条边的长是x,那么第二条边的长是
x+10,但没有明确指明5cm是底边还是腰,因此要分两种情况,分类讨论.
| 2 |
| 3 |
解答:解:设第一条边的长是x,那么第二条边的长是
x+10,
当x为底时,x+2(
x+10)=62,解得x=18,
x+10=22,
18,22,22能够组成三角形;
当x为腰时,2x+(
x+10)=62,解得x=19.5,
x+10=23,
19.5,19.5,23能够组成三角形;
答:这个三角形的边长为18,22,22或19.5,19.5,23.
| 2 |
| 3 |
当x为底时,x+2(
| 2 |
| 3 |
| 2 |
| 3 |
18,22,22能够组成三角形;
当x为腰时,2x+(
| 2 |
| 3 |
| 2 |
| 3 |
19.5,19.5,23能够组成三角形;
答:这个三角形的边长为18,22,22或19.5,19.5,23.
点评:本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
有下列长度的三条线段,能组成等腰三角形的是( )
| A、1cm,1cm,2cm |
| B、1cm,1cm,3cm |
| C、2cm,2cm,4cm |
| D、3cm,3cm,4cm |
 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=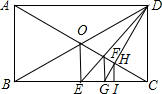 如图,在矩形ABCD中,对角线AC、BD相交于点O.
如图,在矩形ABCD中,对角线AC、BD相交于点O. 如图,在△ABC中,AC的垂直平分线交AC于点E,交BC于点D,△ABD的周长是12cm,则AB+BC=
如图,在△ABC中,AC的垂直平分线交AC于点E,交BC于点D,△ABD的周长是12cm,则AB+BC=