题目内容
10．解方程：（1）$\frac{3}{x}$-$\frac{2}{x+2}$=0
（2）$\frac{5x-4}{x-2}$=$\frac{4x+10}{3x-6}$-1．
分析 两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）去分母得：3x+6-2x=0，
解得：x=-6，
经检验x=-6是分式方程的解；
（2）去分母得：15x-12=4x+10-3x+6，
移项合并得：14x=28，
解得：x=2，
经检验x=2是增根，分式方程无解．
点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
练习册系列答案
相关题目
18．下列运算正确的是（ ）
| A． | 2$\sqrt{3}$+4$\sqrt{2}$=6$\sqrt{5}$ | B． | $\sqrt{8}$=4$\sqrt{2}$ | C． | $\sqrt{3}$•$\sqrt{6}$=3$\sqrt{2}$ | D． | $\sqrt{（-3）^{2}}$=-3 |
2．下列命题中，是真命题的有（ ）
①同旁内角互补；
②若n＜1，则n2-1＜0；
③如果一个角的两边分别与另一个角的两边分别平行，那么这两个角相等；
④同一平面内，如果直线l1⊥l2，直线l2⊥l3，那么l1∥l3．
①同旁内角互补；
②若n＜1，则n2-1＜0；
③如果一个角的两边分别与另一个角的两边分别平行，那么这两个角相等；
④同一平面内，如果直线l1⊥l2，直线l2⊥l3，那么l1∥l3．
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
19．
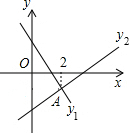如图，直线y1=-x+m与y2=kx+n相交于点A，若点A的横坐标为2，则下列结论中错误的是（ ）
如图，直线y1=-x+m与y2=kx+n相交于点A，若点A的横坐标为2，则下列结论中错误的是（ ）| A． | k＞0 | B． | m＞n | C． | 当x＜2时，y2＞y1 | D． | 2k+n=m-2 |