题目内容
5.先化简,再求值:($\frac{{x}^{2}+4}{x}$-4)÷$\frac{{x}^{2}-4}{{x}^{2}+2x}$,其中x=$\sqrt{2}$+2.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{{x}^{2}-4x+4}{x}$•$\frac{x(x+2)}{(x+2)(x-2)}$=$\frac{(x-2)^{2}}{x}$•$\frac{x(x+2)}{(x+2)(x-2)}$=x-2,
当x=$\sqrt{2}$+2时,原式=$\sqrt{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.已知关于x的方程$\frac{2x+m}{x-2}$=3的解是正数,那么m的取值范围为( )
| A. | m>-6且m≠-2 | B. | m<6 | C. | m>-6且m≠-4 | D. | m<6且m≠-2 |
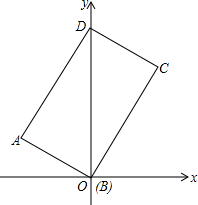 如图,矩形ABCD的对角线BD和y轴重合,已知AB=3,BC=3$\sqrt{3}$,求矩形各顶点的坐标.
如图,矩形ABCD的对角线BD和y轴重合,已知AB=3,BC=3$\sqrt{3}$,求矩形各顶点的坐标.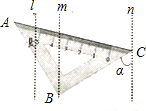 如图,直线l∥m∥n,△ABC的直角顶点B和另一顶点C分别在直线m和n上,边BC与直线n所夹的角∠α为52°,则∠β的度数为38°.
如图,直线l∥m∥n,△ABC的直角顶点B和另一顶点C分别在直线m和n上,边BC与直线n所夹的角∠α为52°,则∠β的度数为38°.