题目内容
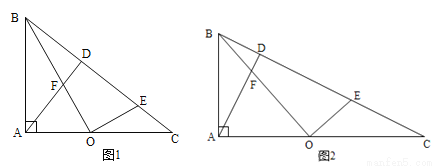
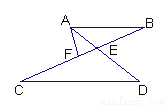
如图1,在Rt△ABC中,∠BAC=90º.AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.
求证:△ABF∽△COE;
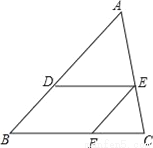
当O为AC边中点,且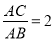 时,如图2,求
时,如图2,求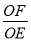 的值;
的值;
当O为AC边中点,且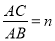 时,直接写出
时,直接写出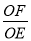 的值.
的值.
练习册系列答案
相关题目
某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.7 | 9.5 | 9.5 | 9.7 |
方差/环2 | 5.1 | 4.7 | 4.5 | 4.5 |
请你根据表中数据选一人参加比赛,最合适的人选是
A. 甲 B. 乙 C. 丙 D. 丁
D 【解析】根据方差的性质可知,方差越小,成绩越稳定,在方差相同情况下,比较平均数,平均数越高,成绩教好,故选D.

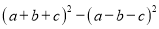
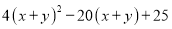
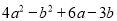
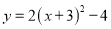 的顶点坐标是( )
的顶点坐标是( )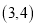 B.
B. 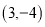 C.
C. 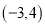 D.
D. 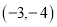
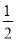 .
.