题目内容
2.当m为什么实数时,关于x的一元二次方程mx2-2(m+1)x+m-1=0的两个根都是正数.分析 由关于x的一元二次方程mx2-2(m+1)x+m-1=0的两个根都是正数.根据一元二次方程的定义和根的判别式的意义可得m≠0且△>0,$\frac{2(m+1)}{m}>$0,$\frac{m-1}{m}>$0,四个不等式的公共解即为m的取值范围.
解答 解:关于x的方程mx2-2(m+1)x+m-1=0是一元二次方程.
∴$\left\{\begin{array}{l}{m≠0}\\{△=[-2(m+1)]^{2}-4m(m-1)≥0}\end{array}\right.$,
∴m>0,
∵方程mx2-2(m+1)x+m-1=0的两个根都是正数,
∴$\frac{2(m+1)}{m}>$0,$\frac{m-1}{m}>$0,
解得:m>1,
∴当m>1时,关于x的一元二次方程mx2-2(m+1)x+m-1=0的两个根都是正数.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根;也考查了一元二次方程的定义.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
12.一个工人生产零件,计划30天完成,若每天多生产5个,则在26天里完成且多生产10个.若设原计划每天生产x个,则这个工人原计划每天生产多少个零件?根据题意可列方程( )
| A. | $\frac{30x-10}{x+5}$=26 | B. | $\frac{30x+10}{x+5}$=26 | C. | $\frac{30x}{x+5}$=26+10 | D. | $\frac{30x+10}{x-5}$=26 |
13.俗话说,登高观远,从理论上讲,当人站在距地面hkm的高处时,能看到的最远距离约为d=112$\sqrt{h}$km,连云港花果山玉女峰高680km,游客站在峰顶最多能看多远?(结果精确到1m).
17.下列计算中,正确的是( )
| A. | $\sqrt{(-9)×(-25)}$=$\sqrt{-9}×\sqrt{-25}$=(-3)×(-5)=15 | B. | -3$\sqrt{\frac{2}{3}}$=$\sqrt{(-3)^{2}×\frac{2}{3}}$=$\sqrt{6}$ | ||
| C. | $\sqrt{1{3}^{2}-1{2}^{2}}$=$\sqrt{(13+12)(13-12)}$=$\sqrt{25}$=5 | D. | 3$\sqrt{2}•4\sqrt{2}=12\sqrt{2}$ |
10.缸内红茶菌的面积每天长大一倍,若17天长满整个缸面,那么经过多少天长满缸面的一半( )
| A. | 8 | B. | 9 | C. | 15 | D. | 16 |
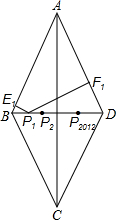 如图,已知菱形ABCD的边AB=10,对角线BD=12,BD边上有2013个不同的点P1,P2,P3…P2013,过Pi(i=1,2,3…)作PiEi于Ei,PiEi于Fi,P1E1+P1F1+P2E2+P2F2+…P2012E2012+P2012F2012+P2013E2013+P2013F2013的值为19324.8.
如图,已知菱形ABCD的边AB=10,对角线BD=12,BD边上有2013个不同的点P1,P2,P3…P2013,过Pi(i=1,2,3…)作PiEi于Ei,PiEi于Fi,P1E1+P1F1+P2E2+P2F2+…P2012E2012+P2012F2012+P2013E2013+P2013F2013的值为19324.8.