题目内容
20．已知单项式xa+2yb+3和3x2a+1y1-b的和仍是单项式，求这两个单项式的和．分析 根据单项式的和是单相识，可得同类项，根据同类项是字母相同且相同字母的指数也相同，可得关于a、b的方程，根据合并同类项，可得答案．
解答 解：由单项式xa+2yb+3和3x2a+1y1-b的和仍是单项式，得
$\left\{\begin{array}{l}{a+2=2a+1}\\{b+3=1-b}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$．
故xa+2yb+3+3x2a+1y1-b=x3y2+3x3y2=4x3y2．
点评 本题考查了同类项，利用同类项的定义得出关于a、b的方程是解题关键，又利用了合并同类项．
练习册系列答案
相关题目
画出三角形所有的中线
小明在一块长18m，宽14m的空地上为班级建造一个花园，所建花园占空地面积的$\frac{1}{2}$，请你求出图中的x．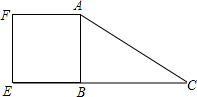
如图所示，△ABC是直角三角形，四边形ABEF是正方形，AC=15，BC=8．
已知，如图，D，E分别是AB，AC上的点，求证；∠3-∠1=∠2-∠4．