题目内容
17.下列方程中没有实数根的是( )| A. | x2+17=8x | B. | 2x2-2$\sqrt{2}$x+1=0 | C. | 5x2-3x=x+1 | D. | x2-4x-7=0 |
分析 根据一元二次方程的根的判别式的取值范围判断即可.
解答 解:A、∵△=64-4×17<0,
∴此方程无实数根;
B、∵△=8-4×2×1=0,
∴此方程有实数根;
C、∵△=16+4×5×1>0,
∴此方程有实数根;
D、∵△16+4×1×7>0,
∴此方程有实数根;
故选A.
点评 本题考查了一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
12.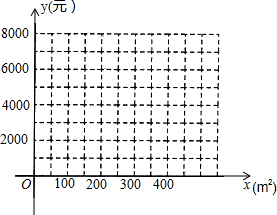 在创建国家卫生城市环境综合整治行动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:
在创建国家卫生城市环境综合整治行动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:
乙公司表示:若该小区先支付3000元的基本承包费,则可按15元/m2的价格收费.请根据以上信息,解答下列问题:
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(x≥100)(m2)满足的函数关系式;
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为800m2,则选择哪家装饰公司进行施工更合算?
 在创建国家卫生城市环境综合整治行动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:
在创建国家卫生城市环境综合整治行动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:| 粉刷面积x(m2) | 100 | 200 | 300 | 400 | … |
| 费用y(元) | 2000 | 4000 | 6000 | 8000 | … |
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(x≥100)(m2)满足的函数关系式;
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为800m2,则选择哪家装饰公司进行施工更合算?

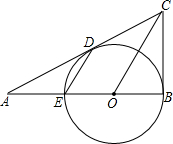 已知:如图,BE是⊙O的直径,CB与⊙O相切于点B,OC∥DE交⊙O于点D,CD的延长线与BE的延长线交于A点.
已知:如图,BE是⊙O的直径,CB与⊙O相切于点B,OC∥DE交⊙O于点D,CD的延长线与BE的延长线交于A点.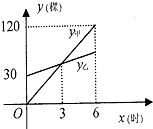 某校甲、乙两班参加植树活动,乙班先植树,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.下列说法正确的有( )
某校甲、乙两班参加植树活动,乙班先植树,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.下列说法正确的有( )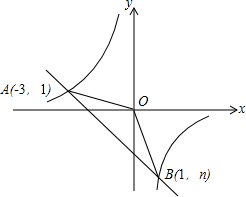 如图.一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象 相交于A、B两点.
如图.一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象 相交于A、B两点. 如图,⊙O的直径AB=8cm,D为⊙O上一点,过点D的切线与AB的延长线于点C.AD=CD,求:
如图,⊙O的直径AB=8cm,D为⊙O上一点,过点D的切线与AB的延长线于点C.AD=CD,求: