题目内容
5.已知三角形的边长分别为4、a、8,则a的取值范围是4<a<12;如果这个三角形中有两条边相等,那么它的周长为20.分析 根据三角形的三边关系可得8-4<a<8+4,再解即可得到a的取值范围;根据三角形的三边关系结合已知条件可得a=8,然后求周长即可.
解答 解:根据三角形的三边关系可得:
8-4<a<8+4,
即4<a<12,
∵这个三角形中有两条边相等,
∴a=8或a=4(不符合三角形的三边关系,不合题意,舍去)
∴周长为4+8+8=20,
故答案为:4<a<12;20.
点评 此题主要考查了三角形的三边关系,关键是掌握三角形两边之和大于第三边;三角形的两边差小于第三边.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
17. 如右图,若AB∥CD,∠1=50°,则∠2的度数是( )
如右图,若AB∥CD,∠1=50°,则∠2的度数是( )
 如右图,若AB∥CD,∠1=50°,则∠2的度数是( )
如右图,若AB∥CD,∠1=50°,则∠2的度数是( )| A. | 50° | B. | 130° | C. | 40° | D. | 145° |
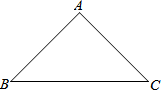 阅读下列材料:
阅读下列材料: 如图:已知AB∥CF,若∠ABC=70°,∠BCD=20°,∠CDE=130°,
如图:已知AB∥CF,若∠ABC=70°,∠BCD=20°,∠CDE=130°,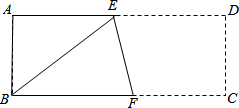 已知,如图长方形ABCD中,AB=a,AD=b,且a、b满足b=$\sqrt{a-3}+\sqrt{6-2a}$+9,将此长方形折叠,使点B与点D重合,折痕为EF,
已知,如图长方形ABCD中,AB=a,AD=b,且a、b满足b=$\sqrt{a-3}+\sqrt{6-2a}$+9,将此长方形折叠,使点B与点D重合,折痕为EF,