题目内容
18.如图所示.
(1)若线段AB=4cm,点C在线段AB上(如图①),点M、N分别是线段AC、BC的中点,求线段MN长.
(2)若线段AB=acm,点C在线段AB的延长线上(如图②),点M、N分别是线段AC、BC的中点,你能猜想出MN的长度吗?请写出你的结论,并说明理由.
分析 (1)先根据点M,N分别是AC、BC的中点得出MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC,再根据MN=MC+NC即可得出结论;
(2)先根据点M,N分别是AC、BC的中点得出MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC,再根据MN=MC-NC即可得出结论;
解答 解:(1)∵点M,N分别是AC、BC的中点,AB=4cm,
∴MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC,
∴MN=MC+NC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB=$\frac{1}{2}$×4cm=2cm;
(2)MN=$\frac{1}{2}$acm,
理由是:∵点M,N分别是AC、BC的中点,AB=acm,
∴MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC,
∴MN=MC-NC=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$AB=$\frac{1}{2}$×acm=$\frac{1}{2}$acm.
点评 本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
相关题目
9.若点P关于x轴的对称点为P1(2a+b,3),关于y轴的对称点为P2(9,b+2),则点P的坐标为( )
| A. | (9,3) | B. | (-9,3) | C. | (9,-3) | D. | (-9,-3) |
3.分式方程$\frac{2}{x-3}$=$\frac{5}{4x}$的根是( )
| A. | x=-5 | B. | x=2 | C. | x=4 | D. | x=5 |
7.多项式A=2(m2-3mn-n2),B=m2+2amn+2n2,如果A-B中不含mn项,则a的值为( )
| A. | -3 | B. | -4 | C. | 3 | D. | -2 |
 仔细看看,认真想想,怎样画出如图所示的图案.
仔细看看,认真想想,怎样画出如图所示的图案.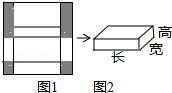 图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,这个长方体的高为5cm.
图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,这个长方体的高为5cm. 如图,在△ABC中,AC=BC,点O是AC上一动点,以O为圆心,OA的长为半径的圆与AB交于点D,作DE⊥BC,垂足为点E,试判断DE与⊙O的位置关系,并说明理由.
如图,在△ABC中,AC=BC,点O是AC上一动点,以O为圆心,OA的长为半径的圆与AB交于点D,作DE⊥BC,垂足为点E,试判断DE与⊙O的位置关系,并说明理由.