题目内容
在△ABC中，若∠A：∠B：∠C=1：2：3，则∠B= ．
考点：三角形内角和定理
专题：
分析：根据比例设∠A=k，∠B=2k，∠C=3k，然后利用三角形的内角和定理列出方程求解k，然后求解即可．
解答：解：∵∠A：∠B：∠C=1：2：3，
∴设∠A=k，∠B=2k，∠C=3k，
由三角形的内角和定理得，k+2k+3k=180°，
解得k=30°，
∴∠B=2×30°=60°．
故答案为：60°．
∴设∠A=k，∠B=2k，∠C=3k，
由三角形的内角和定理得，k+2k+3k=180°，
解得k=30°，
∴∠B=2×30°=60°．
故答案为：60°．
点评：本题考查了三角形的内角和定理，利用“设k法”表示出三角形的三个内角求解更简便．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
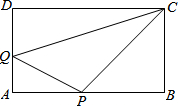如图：在矩形ABCD中，AB=12cm，BC=6cm，点P沿AB边从A开始向点B以2厘米/秒的速度移动，点Q沿DA边从D开始向点A以1厘米/秒的速度移动，如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6）．