题目内容
1.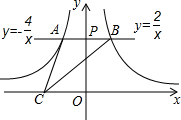 如图,反比例函数y=$\frac{k_1}{x}$和y=$\frac{k_2}{x}$的图象与过y轴正半轴上任意一点M且平行于x轴的直线交于点A和点B,点C是x轴上任意一点,连接AC、BC,若△ABC的面积为8,则k2-k1的值是16.
如图,反比例函数y=$\frac{k_1}{x}$和y=$\frac{k_2}{x}$的图象与过y轴正半轴上任意一点M且平行于x轴的直线交于点A和点B,点C是x轴上任意一点,连接AC、BC,若△ABC的面积为8,则k2-k1的值是16.
分析 先设P(0,b),由直线AB∥x轴,则A,B两点的纵坐标都为b,而A,B分别在反比例函数y=$\frac{k_1}{x}$和y=$\frac{k_2}{x}$的图象上,可得到A点坐标为($\frac{{k}_{1}}{b}$,b),B点坐标为($\frac{{k}_{2}}{b}$,b),从而求出AB=$\frac{{k}_{2}-{k}_{1}}{b}$,
,然后根据三角形的面积公式得出$\frac{1}{2}$•$\frac{{k}_{2}-{k}_{1}}{b}$•b=8,即可求得结论.
解答 解:设P(0,b),
∵直线AB∥x轴,
∴A,B两点的纵坐标都为b,而点A在反比例函数y=$\frac{k_1}{x}$的图象上,
∴当y=b,x=$\frac{{k}_{1}}{b}$,即A点坐标为($\frac{{k}_{1}}{b}$,b),
又∵点B在反比例函数y=$\frac{k_2}{x}$的图象上,
∴当y=b,x=$\frac{{k}_{2}}{b}$,即B点坐标为($\frac{{k}_{2}}{b}$,b),
∴AB=$\frac{{k}_{2}}{b}$-$\frac{{k}_{1}}{b}$=$\frac{{k}_{2}-{k}_{1}}{b}$,
∵S△ABC=$\frac{1}{2}$•AB•OP=$\frac{1}{2}$•$\frac{{k}_{2}-{k}_{1}}{b}$•b=8,
∴k2-k1=16.
故答案为:16.
点评 本题考查的是反比例函数系数k的几何意义以及反比例函数图象上点的坐标特征,即在反比例函数的图象上任意一点的坐标符合解析式.

练习册系列答案
相关题目
20. 如图,EF∥MN,AC,BD交于点O,且分别平分∠FAB,∠ABN,图中与∠1互余的角有( )
如图,EF∥MN,AC,BD交于点O,且分别平分∠FAB,∠ABN,图中与∠1互余的角有( )
 如图,EF∥MN,AC,BD交于点O,且分别平分∠FAB,∠ABN,图中与∠1互余的角有( )
如图,EF∥MN,AC,BD交于点O,且分别平分∠FAB,∠ABN,图中与∠1互余的角有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.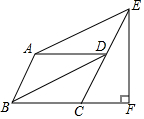 如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
 如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
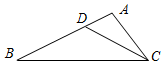 如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )
如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )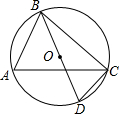 如图,⊙O的直径BD=4,∠A=60°,则CD的长度为2.
如图,⊙O的直径BD=4,∠A=60°,则CD的长度为2.