题目内容
12.圆柱的轴截面平行于投影面S,它的正投影是长4,宽3的矩形,则这个圆柱的表面积是20π.(结果保留π)分析 根据平行投影的性质得出圆柱体底面圆的半径为2,高为3,进而求出其表面积.
解答 解:∵一个圆柱的轴截面平行于投影面,圆柱的正投影是长4,宽3的矩形,
∴圆柱底面圆的半径为2,高为3,
则圆柱的表面积为:2π×2×3+2π×22=12π+8π=20π,
故答案为:20π.
点评 此题主要考查了平行投影以及圆柱体的表面积公式,得出圆柱体的底面圆的半径是解题关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
7.当某一几何体在投影面P前的摆放位置确定以后,改变它与投影面P的距离,其正投影的形状( )
| A. | 不发生变化 | B. | 变大 | C. | 变小 | D. | 无法确定 |
4.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是二元一次方程mx+3y=2的一组解,则m的值为( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | 2 |
1.下列方程是二元一次方程的是( )
| A. | xy=3 | B. | $\frac{x}{2}$+$\frac{y}{2}$=3 | C. | $\frac{2}{x}$+$\frac{2}{y}$=3 | D. | 2x+$\frac{2}{y}$=3 |
2.下列几何体中,主视图和俯视图都为矩形的是( )
| A. |  | B. | 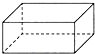 | C. |  | D. | 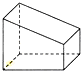 |