题目内容
17.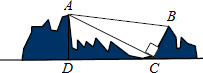 如图,某景区有一出索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,求山峰顶点A到C点的水平面高度AD.(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)
如图,某景区有一出索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,求山峰顶点A到C点的水平面高度AD.(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)
分析 在直角三角形ABC中,由AB与BC的长,利用勾股定理求出AC的长,在直角三角形ACD中,利用锐角三角函数定义求出AD的长即可.
解答 解:在Rt△ABC中,BC=500米,AB=1300米,
根据勾股定理得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=1200米,
在Rt△ADC中,sin∠ACD=$\frac{AD}{AC}$,
则AD=AC•sin∠ACD=1200×0.40=480(米).
点评 此题考查了解直角三角形的应用-仰角俯角问题,熟练掌握勾股定理及锐角三角函数定义是解本题的关键.

练习册系列答案
相关题目
5.不等式x-2>1的解集是( )
| A. | x>1 | B. | x>2 | C. | x>3 | D. | x>4 |
8.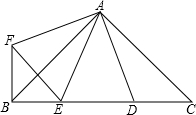 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )
 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )| A. | △AED≌△AEF | B. | △ABE∽△ACD | C. | BE+DC>DE | D. | BE2+DC2=DE2 |
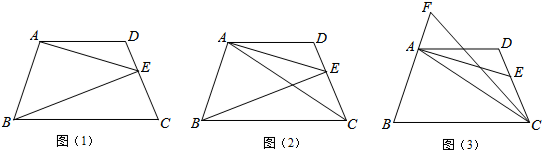
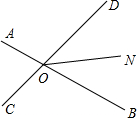 如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠AON的度数为145度.
如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠AON的度数为145度.