题目内容
已知关于x的一元二次方程:x2-2(m+1)x+m2+5=0有两个不相等的实数根.
(1)求m的取值范围;
(2)如果原方程的两个实数根为x1、x2,且满足(x1-x2)2=|x1|+|x2|,求m的值.
(1)求m的取值范围;
(2)如果原方程的两个实数根为x1、x2,且满足(x1-x2)2=|x1|+|x2|,求m的值.
考点:根的判别式,根与系数的关系
专题:
分析:(1)根据方程x2-2(m+1)x+m2+5=0有两个不相等的实数根,得出△>0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=2(m-1),x1x2=m2+5≥0,即两个根同号,再分两种情况讨论,当x1≥0,x2≥0和当x1≤0,x2≤0时,得到一个方程,求出m的值即可.
(2)根据根与系数的关系得到x1+x2=2(m-1),x1x2=m2+5≥0,即两个根同号,再分两种情况讨论,当x1≥0,x2≥0和当x1≤0,x2≤0时,得到一个方程,求出m的值即可.
解答:解:(1)∵x2-2(m+1)x+m2+5=0有两个不相等的实数根,
∴△=[-2(m+1)]2-4×1×(m2+5)>0,
∴m>2;
(2)根据题意得:x1+x2=2(m-1),x1x2=m2+5≥0,
∵(x1-x2)2=|x1|+|x2|,
∴当x1≥0,x2≥0,(x1-x2)2=x1+x2,则(x1+x2)2-4x1x2=x1+x2,4(m-1)2-4(m2+5)=2(m-1),
解得m=-
;
当x1≤0,x2≤0,(x1-x2)2=-(x1+x2),则(x1+x2)2-4x1x2=-(x1+x2),4(m-1)2-4(m2+5)=-2(m-1),
解得m=-3;
则m的值为-
或-3.
∴△=[-2(m+1)]2-4×1×(m2+5)>0,
∴m>2;
(2)根据题意得:x1+x2=2(m-1),x1x2=m2+5≥0,
∵(x1-x2)2=|x1|+|x2|,
∴当x1≥0,x2≥0,(x1-x2)2=x1+x2,则(x1+x2)2-4x1x2=x1+x2,4(m-1)2-4(m2+5)=2(m-1),
解得m=-
| 7 |
| 5 |
当x1≤0,x2≤0,(x1-x2)2=-(x1+x2),则(x1+x2)2-4x1x2=-(x1+x2),4(m-1)2-4(m2+5)=-2(m-1),
解得m=-3;
则m的值为-
| 7 |
| 5 |
点评:本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
若x=-2,则|x-3|的值是( )
| A、1 | B、-1 | C、5 | D、-5 |
比a的3倍小2的数是( )
| A、3a+2 |
| B、3a-2 |
| C、3(a+2) |
| D、3(a-2) |
一天早晨的气温是-4℃,中午上升了8℃,晚上又下降了6℃,则晚上的气温是( )
| A、2℃ | B、-2℃ |
| C、-6℃ | D、6℃ |
 如图,在△ABC的顶点A的直线上取两点D、E,连接BD、CE,已知∠1=∠2,∠3=∠4,∠5=∠6;求证:BD∥AC.
如图,在△ABC的顶点A的直线上取两点D、E,连接BD、CE,已知∠1=∠2,∠3=∠4,∠5=∠6;求证:BD∥AC.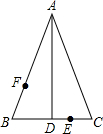 如图,AD是等腰△ABC的顶角平分线,E、F分别是DC、AB上的点,求作点E、F关于
如图,AD是等腰△ABC的顶角平分线,E、F分别是DC、AB上的点,求作点E、F关于 如图,一个平行四边形的底为a,高为h,根据下列条件求它的面积S.
如图,一个平行四边形的底为a,高为h,根据下列条件求它的面积S. 如图是某产品的商标图案,求阴影部分的面积.
如图是某产品的商标图案,求阴影部分的面积.