题目内容
若二次函数y=ax2+bx+c的图象经过(3,5),且方程ax2+bx+c=0的两实根为x1=1,x2=-2,求该二次函数的表达式.
考点:待定系数法求二次函数解析式
专题:计算题
分析:根据抛物线与x轴的交点问题得到抛物线过点(1,0),(-2,0),则可设交点式y=a(x-1)(x+2),然后把(3,5)代入求出a即可.
解答:解:∵方程ax2+bx+c=0的两实根为x1=1,x2=-2,
∴抛物线过点(1,0),(-2,0),
设抛物线解析式为y=a(x-1)(x+2),
把(3,5)代入得a•(3-1)(3+2)=5,解得a=
,
∴抛物线解析式为y=
(x-1)(x+2)=
x2+
x-1.
∴抛物线过点(1,0),(-2,0),
设抛物线解析式为y=a(x-1)(x+2),
把(3,5)代入得a•(3-1)(3+2)=5,解得a=
| 1 |
| 2 |
∴抛物线解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
互为余角的两个角之比是2:3,则这两个角分别是( )
| A、72°,108° |
| B、38°,52° |
| C、40°,60° |
| D、36°,54° |
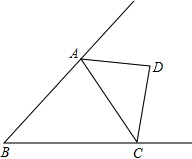 如图,点D是△ABC的两外角平分线的交点,下列说法:
如图,点D是△ABC的两外角平分线的交点,下列说法:①AD=CD; ②点D到AB、BC所在直线的距离相等;
③点D到三边AB、BC、AC所在直线的距离相等;④点D在∠B的平分线上.
其中正确的是( )
| A、②④④ | B、①②④ |
| C、②③④ | D、①②③④ |
下列根式是最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若x=-2,则|x-3|的值是( )
| A、1 | B、-1 | C、5 | D、-5 |
比a的3倍小2的数是( )
| A、3a+2 |
| B、3a-2 |
| C、3(a+2) |
| D、3(a-2) |
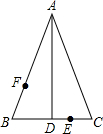 如图,AD是等腰△ABC的顶角平分线,E、F分别是DC、AB上的点,求作点E、F关于
如图,AD是等腰△ABC的顶角平分线,E、F分别是DC、AB上的点,求作点E、F关于 如图,一个平行四边形的底为a,高为h,根据下列条件求它的面积S.
如图,一个平行四边形的底为a,高为h,根据下列条件求它的面积S.