题目内容
18.计算:(1)$\frac{a+2}{{a}^{2}-2a}$•$\frac{{a}^{2}-4a+4}{a+2}$
(2)$\frac{1}{a-1}$-1-a
(3)$\frac{{x}^{2}+1}{x-2}$-$\frac{3-4x}{2-x}$;
(4)($\frac{1}{{x}^{2}-2x}$-$\frac{1}{{x}^{2}-4x+4}$)÷$\frac{2}{{x}^{2}-2x}$.
分析 (1)原式约分即可得到结果;
(2)原式通分并利用同分母分式的减法法则计算即可得到结果;
(3)原式变形后,利用同分母分式的加法法则计算即可得到结果;
(4)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=$\frac{a+2}{a(a-2)}$•$\frac{(a-2)^{2}}{a+2}$=$\frac{a-2}{a}$;
(2)原式=$\frac{1-(a+1)(a-1)}{a-1}$=$\frac{2-{a}^{2}}{a-1}$;
(3)原式=$\frac{{x}^{2}+1+3-4x}{x-2}$=$\frac{(x-2)^{2}}{x-2}$=x-2;
(4)原式=$\frac{x-2-x}{x(x-2)^{2}}$•$\frac{x(x-2)}{2}$=-$\frac{1}{2x-4}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列调查中,调查方式选择正确的是( )
| A. | 为了解10000个灯泡的使用寿命,选择普查 | |
| B. | 为了解某鱼塘中鱼的质量,选择普查 | |
| C. | 为了解某班级学生的视力情况,选择普查 | |
| D. | 为了解一批袋装食品是否有防腐剂,选择普查 |
6.已知一次函数y=kx+3,当x=-1时,y=-1,那么当x=1时,y等于( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
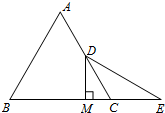 如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,
如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M, 如图在平行四边形的纸片上有一个圆洞,请画一条直线把纸片分成分成面积相等的两部分.
如图在平行四边形的纸片上有一个圆洞,请画一条直线把纸片分成分成面积相等的两部分.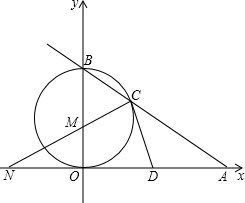 如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.
如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM.