题目内容
10.以矩形ABCD的顶点A为圆心画⊙A,使得B、C、D中至少有一点在⊙A内,且至少有一点在⊙A外,若BC=8,CD=6.则⊙A的半径r的取值范围是6<r<10.分析 连接AC,根据勾股定理求出AC,再根据题意得出B在圆内,C在圆外,根据AB和AC的长即可得出答案.
解答 解:如图,连接AC,
∵四边形ABCD是矩形,
∴∠B=90°,AB=DC=6,AD=BC=8,
由勾股定理得:AC=10,
∴AC>AD>AB,
∵以矩形ABCD的顶点A为圆心画⊙A,使得B、C、D中至少有一点在⊙A内,且至少有一点在⊙A外,
∴6<r<10.
故答案为:6<r<10.
点评 本题考查了勾股定理,矩形的性质,点和圆的位置关系的应用,能正确运用点和圆的位置关系分析问题是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列调查,最适合使用普查方式的是( )
| A. | 为制作校服,了解某班同学的身高情况 | |
| B. | 了解全市每天丢弃的废旧电池数 | |
| C. | 了解某批炮弹的杀伤半径 | |
| D. | 了解我省农民的年人均收入情况 |
2.关于等边三角形,下列说法中错误的是( )
| A. | 等边三角形中,各边都相等 | |
| B. | 等边三角形是特殊的等腰三角形 | |
| C. | 三个角都等于60°的三角形是等边三角形 | |
| D. | 有一个角为60°的等腰三角形不是等边三角形 |
5.下列命题错误的是( )
| A. | 经过不在同一直线上的三个点一定可以作圆 | |
| B. | 三角形的外心到三角形各顶点的距离相等 | |
| C. | 经过切点且垂直于切线的直线必经过圆心 | |
| D. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 |
18.计算:(x4)2÷x2的结果是( )
| A. | x3 | B. | x4 | C. | x5 | D. | x6 |
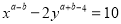 是二元一次方程,那么
是二元一次方程,那么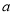 、
、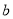 的值分别是( )
的值分别是( )