题目内容
7. 在△ABC中,∠B=58°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=61°.
在△ABC中,∠B=58°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=61°.
分析 根据三角形内角和定理、角平分线的定义以及三角形外角定理求得$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF=$\frac{1}{2}$(∠B+∠B+∠1+∠2)=119°;最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数.
解答 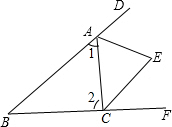 解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC=$\frac{1}{2}$∠DAC,∠ECA=$\frac{1}{2}$∠ACF,
∵∠DAC=∠B+∠2,∠ACF=∠B+∠1
∴$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF=$\frac{1}{2}$(∠B+∠2)+$\frac{1}{2}$(∠B+∠1)=$\frac{1}{2}$(∠B+∠B+∠1+∠2),
∵∠B=58°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF=119°
∴∠AEC=180°-($\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF)=61°.
故答案是:61°.
点评 本题考查了三角形内角和定理、三角形外角性质.解题时注意挖掘出隐含在题干中已知条件“三角形内角和是180°”.

练习册系列答案
相关题目
17.弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下:
(1)求L与x之间的函数关系;
(2)请估计重物为5kg时弹簧总长L(cm)是多少?
| 弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
| 重物质量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
(2)请估计重物为5kg时弹簧总长L(cm)是多少?
16.若反比例函数y=$\frac{k}{x}$的图象经过点(-3,2),则该反比例函数的图象在( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
 如图,在Rt△ABC中,AB=10cm,sinA=$\frac{3}{5}$.如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s,点Q的速度为1cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5)
如图,在Rt△ABC中,AB=10cm,sinA=$\frac{3}{5}$.如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s,点Q的速度为1cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5) 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a>0;②c>0;③a+b+c<0;④2+2a<0.其中所有正确结论的序号是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a>0;②c>0;③a+b+c<0;④2+2a<0.其中所有正确结论的序号是( ) 如图所示,矩形中,AB=2,AD=3,点P为BC上与点B、C不重合的任意一点,设PA=x,D到AP的距离为y,则y与x的函数关系式为y=$\frac{6}{x}$.
如图所示,矩形中,AB=2,AD=3,点P为BC上与点B、C不重合的任意一点,设PA=x,D到AP的距离为y,则y与x的函数关系式为y=$\frac{6}{x}$. 在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.
在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP. 如图,AD⊥DB,BC⊥CA,AC、BD相交于O,且AC=BD.求证:OD=OC.
如图,AD⊥DB,BC⊥CA,AC、BD相交于O,且AC=BD.求证:OD=OC.