题目内容
16. 如图,在菱形ABCD中,对角线AC、BD相交于点O,∠BAD=120°,AC=8cm,则菱形ABCD面积是32$\sqrt{3}$ cm2.
如图,在菱形ABCD中,对角线AC、BD相交于点O,∠BAD=120°,AC=8cm,则菱形ABCD面积是32$\sqrt{3}$ cm2.
分析 由菱形的性质得出AB=BC,OA=$\frac{1}{2}$AC=4cm,OB=$\frac{1}{2}$BD,AC⊥BD,∠BAD+∠ABC=180°,再证明△ABC是等边三角形,得出AB=AC=8,根据勾股定理求出OB,得出BD,由菱形的面积=$\frac{1}{2}$AC•BD,即可得出结论.
解答 解:∵四边形ABCD是菱形,
∴AB=BC,OA=$\frac{1}{2}$AC=4cm,OB=$\frac{1}{2}$BD,AC⊥BD,∠BAD+∠ABC=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=8cm,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$(cm),
∴BD=2OB=8$\sqrt{3}$cm,
∴菱形ABCD的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×8×8$\sqrt{3}$=32$\sqrt{3}$;
故答案为:32$\sqrt{3}$.
点评 本题考查了菱形的性质、等边三角形的判定与性质、勾股定理、菱形面积的计算;熟练掌握菱形的性质,运用勾股定理求出OB是解决问题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
1.在-3,0,-2,1四个数中,最小的数是( )
| A. | -3 | B. | 0 | C. | -2 | D. | 1 |
5.下列计算正确的是( )
| A. | -33=-27 | B. | (-4)2=-16 | C. | (-$\frac{1}{5}$)3=$\frac{1}{125}$ | D. | (-$\frac{1}{3}$)4=-$\frac{4}{3}$ |
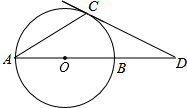 如图,已知在⊙0中,直径AB与弦AC的夹角是30°,过C点的切线交AB的延长线于D,AC=$\sqrt{6}$cm,求CD的长.
如图,已知在⊙0中,直径AB与弦AC的夹角是30°,过C点的切线交AB的延长线于D,AC=$\sqrt{6}$cm,求CD的长.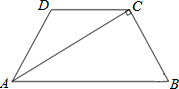 如图,在梯形ABCD中,AB∥DC,AD=BC,∠D=120°,AC⊥BC,求tan∠DAC的值.
如图,在梯形ABCD中,AB∥DC,AD=BC,∠D=120°,AC⊥BC,求tan∠DAC的值.