题目内容
10.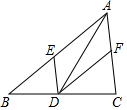 在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是( )
在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD⊥BC,那么四边形AEDF是菱形 | |
| D. | 如果AD平分∠BAC,那么四边形AEDF是菱形 |
分析 根据平行四边形、矩形、菱形的判定方法一一判断即可.
解答  解:由DE∥CA,DF∥BA,根据两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形;
解:由DE∥CA,DF∥BA,根据两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形;
又有∠BAC=90°,根据有一角是直角的平行四边形是矩形,可得四边形AEDF是矩形.故A、B正确;
如果AD平分∠BAC,那么∠EAD=∠FAD,又有DF∥BA,可得∠EAD=∠ADF,
∴∠FAD=∠ADF,
∴AF=FD,那么根据邻边相等的平行四边形是菱形,可得四边形AEDF是菱形,故D正确;
故选C.
点评 本题考查平行四边形、矩形、菱形的判定等知识,解题的关键是熟练掌握特殊四边形的判定方法,属于中考常考题型.

练习册系列答案
相关题目
18.下列轴对称图形中,对称轴条数最多的图形是( )
| A. | 等腰三角形 | B. | 正三角形 | C. | 菱形 | D. | 等腰梯形 |
5.若m>n,则下列不等式不正确的是( )
| A. | m±c>n±c | B. | 6m>6n | C. | mc>nc | D. | 6m+c>6n+c |
2.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{3}$-3$\sqrt{3}$=1 | C. | $\sqrt{18}$÷$\sqrt{2}$=3 | D. | 3$\sqrt{2}$×2$\sqrt{2}$=6$\sqrt{2}$ |
 某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题:
某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题: