题目内容
20.解答下列各题:(1)(-12)-5+(-14)-(-39)
(2)3$\frac{1}{2}$-(-$\frac{1}{3}$)+2$\frac{2}{3}$+(-$\frac{1}{2}$)
(3)$\frac{2}{5}$-|-1$\frac{1}{2}$|-(+2$\frac{1}{4}$)-(-2.75)
分析 (1)先化简,再计算加减法;
(2)先计算同分母分数,再相加即可求解;
(3)先计算绝对值,再计算同分母分数,再相加即可求解.
解答 解:(1)(-12)-5+(-14)-(-39)
=-12-5-14+39
=-31+39
=8;
(2)3$\frac{1}{2}$-(-$\frac{1}{3}$)+2$\frac{2}{3}$+(-$\frac{1}{2}$)
=(3$\frac{1}{2}$-$\frac{1}{2}$)+($\frac{1}{3}$+2$\frac{2}{3}$)
=3+3
=6;
(3)$\frac{2}{5}$-|-1$\frac{1}{2}$|-(+2$\frac{1}{4}$)-(-2.75)
=$\frac{2}{5}$-1$\frac{1}{2}$+(-2$\frac{1}{4}$+2.75)
=$\frac{2}{5}$-1$\frac{1}{2}$+$\frac{1}{2}$
=$\frac{2}{5}$+(-1$\frac{1}{2}$+$\frac{1}{2}$)
=$\frac{2}{5}$-1
=-$\frac{3}{5}$.
点评 考查了有理数加减混合运算,方法指引:
①在一个式子里,有加法也有减法,根据有理数减法法则,把减法都转化成加法,并写成省略括号的和的形式.
②转化成省略括号的代数和的形式,就可以应用加法的运算律,使计算简化.

练习册系列答案
相关题目
9.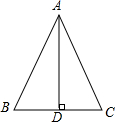 如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )
如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )
 如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )
如图,AD⊥BC,且AB=AC,则判定△ABD≌△ACD的最好理由是( )| A. | ASA | B. | SAS | C. | SSS | D. | HL |
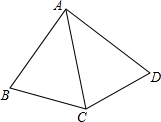 如图,在四边形ABCD中,AC平分∠BAD,AC2=AB•AD.试说明∠BCD=∠B+∠D的理由.
如图,在四边形ABCD中,AC平分∠BAD,AC2=AB•AD.试说明∠BCD=∠B+∠D的理由. 如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=$\frac{4}{3}$,则t的值为3.
如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=$\frac{4}{3}$,则t的值为3.