题目内容
3.△ABC是等边三角形,点P是直线AB上一点,作PE⊥AC于E,点Q为直线BC上一点,PQ交直线AC于点D,DE=$\frac{1}{2}$AB.(1)如图1,若点P在边AB上,点Q在边BC延长线上,请问AP与CQ有怎样的数量关系,直接写出结论;
(2)如图2,若点P在边AB延长上,点Q在边BC延长线上,(1)问中的结论是否成立,请说明理由;
(3)如图3,若点P在边BA的延长线上,点Q在边BC上,且PQ⊥BC,若CQ=4,求AE的长.

分析 (1)根据等边三角形的性质得到∠A=∠B=∠ACB=60°,AB=AC,如图1,过P作PG∥BC,根据平行线的性质得到∠AGP=∠ACB=60°,∠PGD=∠QCD,推出△APG是等边三角形,于是得到AP=PG证得△PGD≌△QCD,根据全等三角形的性质即可得到结论;
(2)如图2,过P作PF∥BC交AC的延长线于F,根据等边三角形的性质得到∠A=∠B=∠ACB=60°,AB=AC,于是得到∠F=∠ACB=60°,推出△APF是等边三角形,根据等边三角形的性质得到AP=PF,推出△PFD≌△QCD,根据全等三角形的性质即可得到结论.
(3)如图3,过P作PF∥BC交CA的延长线于F,由△ABC是等边三角形,得到AB=AB=BC,由PE⊥AE,△APF是等边三角形,于是得到EF=AE,证得DF=CD,求得CD=DF=8,推出△DQC≌△DPF,根据全等三角形的性质即可得到结论.
解答  解:(1)AP=CQ,
解:(1)AP=CQ,
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,AB=AC,
如图1,过P作PG∥BC,
∴∠AGP=∠ACB=60°,∠PGD=∠QCD,
∴△APG是等边三角形,
∴AP=PG,
∵PE⊥AG,
∴AE=EG,
∵DE=$\frac{1}{2}$AB,
∴AE+CD=$\frac{1}{2}$AB=$\frac{1}{2}$AC,
∴DG=CD,
在△PGD与△CDQ中,$\left\{\begin{array}{l}{∠PGD=∠QCD}\\{GD=CD}\\{∠PDG=∠CDQ}\end{array}\right.$,
∴△PGD≌△QCD,
∴PG=CQ,
∴AP=CQ;
(2)(1)问中的结论成立,
理由:如图2,过P作PF∥BC交AC的延长线于F,
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,AB=AC,
∴∠F=∠ACB=60°,
∴△APF是等边三角形,
∴AP=PF,
∵PE⊥AC,
∴AE=EF,
∵DE=$\frac{1}{2}$AB,
∴DE=$\frac{1}{2}$AC,
∴CD=DE-CE=$\frac{1}{2}$AC-(AC-AE)=AE-$\frac{1}{2}$AC=EF-DE=DF,
即CD=DF,
∵PF∥BQ,
∴∠F=∠QCD,
在△PFD与△QCD中,$\left\{\begin{array}{l}{∠F=∠QCD}\\{CD=DF}\\{∠QDC=∠PDQ}\end{array}\right.$,
∴△PFD≌△QCD,
∴PF=CQ,
∴AP=CQ;
(3)如图3,过P作PF∥BC交CA的延长线于F,
∵△ABC是等边三角形,
∴AB=AB=BC,
∵PE⊥AE,△APF是等边三角形,
∴EF=AE,
∵ED=DF-EF=DF-$\frac{1}{2}$AF=$\frac{1}{2}$AB=$\frac{1}{2}$AC,
∴DF=$\frac{1}{2}$AF+$\frac{1}{2}$AC=$\frac{1}{2}$(AF+AC)=$\frac{1}{2}$CF,
∴DF=CD,
在Rt△DQC中,
∵QC=4,∠CDQ=30°,
∴CD=DF=8,
在△DQC与△DPF中,$\left\{\begin{array}{l}{∠F=∠C}\\{DF=CD}\\{∠PDF=∠CDQ}\end{array}\right.$,
∴△DQC≌△DPF,
∴PF=CQ=AF=4,
∴AE=$\frac{1}{2}$AF=2.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,平行线的性质,正确的作出辅助线是解题的关键.

 小学教材全测系列答案
小学教材全测系列答案| A. | 2乘以16 | B. | 2个16相乘 | C. | 16个2相加 | D. | 16个2相乘 |
 如图所示,从正面看该几何体的图形应为( )
如图所示,从正面看该几何体的图形应为( )| A. |  | B. |  | C. |  | D. |  |
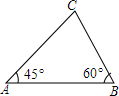 如图,△ABC中,∠A=45°,∠B=60°,AB=100cm,求△ABC的面积.
如图,△ABC中,∠A=45°,∠B=60°,AB=100cm,求△ABC的面积.