题目内容

18．试比较$\sqrt{2015}$-$\sqrt{2014}$，$\sqrt{2014}$-$\sqrt{2013}$的大小，并说明理由．

分析 首先求出$\sqrt{2015}$-$\sqrt{2014}$，$\sqrt{2014}$-$\sqrt{2013}$的倒数的大小，进而判断出它们的倒数的大小关系；然后根据谁的倒数越大，则谁越小，判断出$\sqrt{2015}$-$\sqrt{2014}$，$\sqrt{2014}$-$\sqrt{2013}$的大小即可．

解答 解：$\frac{1}{\sqrt{2015}-\sqrt{2014}}=\frac{\sqrt{2015}+\sqrt{2014}}{（\sqrt{2015}-\sqrt{2014}）（\sqrt{2015}+\sqrt{2014}）}$=$\sqrt{2015}+\sqrt{2014}$，
$\frac{1}{\sqrt{2014}-\sqrt{2013}}$=$\frac{\sqrt{2014}+\sqrt{2013}}{（\sqrt{2014}-\sqrt{2013}）（\sqrt{2014}+\sqrt{2013}）}$=$\sqrt{2014}+\sqrt{2013}$，
∵$\sqrt{2015}$+$\sqrt{2014}＞\sqrt{2014}+\sqrt{2013}$，
∴$\sqrt{2015}$-$\sqrt{2014}$＜$\sqrt{2014}$-$\sqrt{2013}$．

点评 此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是判断出它们的倒数的大小关系．

练习册系列答案
相关题目
8．一列火车在相距270千米的两地之间往返行驶，速度为180千米/时，为了提高运输效率，计划将每往返一趟行驶时间缩短45分钟，这列火车的速度应提高多少？
9．解方程：
（1）-$\frac{1}{2}$x2+$\frac{5}{2}$x-$\frac{5}{4}$=0（用配方法）；
（2）3x2-6x+12=0（公式法）
（3）4x（2x+1）=3（2x+1）（因式分解）
6．一次函数y=kx+b的图象经过点A（2，3），每当x增加1个单位时，y增加3个单位，则此函数表达式是（　　）
A．y=x+3B．y=2x-3C．y=3x-3D．y=4x-4
13．阅读理解题：我们知道因式分解与整式乘法是互逆的关系，那么逆用乘法公式（x+a）（x+b）=x2+（a+b）x+ab，
即x2+（a+b）x+ab=（x+a）（x+b）是否可以分解因式呢？当然可以，而且也很简单．
如：（1）x2+4x+3=x2+（1+3）x+1×3=（x+1）（x+3）；
（2）x2-4x-5=x2+（1-5）x+1×（-5）=（x+1）（x-5）．
请你仿照上述方法，把多项式分解因式：x2-7x-18．
3．如图所示：AD平分∠BAC交BC于D，写出四条线段AB、BD、CD、AC之间的等量关系式$\frac{AB}{AC}=\frac{BD}{CD}$并证明你的结论．
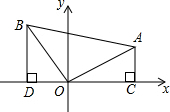10．△ABO为等腰直角三角形，斜边AB=4，过A作AC⊥x轴于C，AC=$\frac{1}{2}$AO，则点A的坐标是（2，$\sqrt{2}$），点B的坐标是（-$\sqrt{2}$，2）．
7．在△ABC中，BC=a，AC=b，AB=c，设c为最长边．当a2+b2=c2时，△ABC是直角三角形；当a2+b2≠c2时，利用代数式a2+b2和c2的大小关系，可以判断△ABC的形状（按角分类）．
（1）请你通过画图探究并判断：当△ABC三边长分别为6，8，9时，△ABC为锐角三角形；当△ABC三边长分别为6，8，11时，△ABC为钝角三角形．
（2）小明同学根据上述探究，有下面的猜想：“当a2+b2＞c2时，△ABC为锐角三角形；当a2+b2＜c2时，△ABC为钝角三角形．”请你根据小明的猜想完成下面的问题：
当a=2，b=3时，最长边c在什么范围内取值时，△ABC是直角三角形、锐角三角形、钝角三角形？
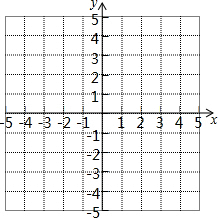5．如图，描出A（-3，-2）、B（2，-2）、C（-2，1）、D（3，1）四个点，线段AB、CD有什么关系？顺次连接A、B、C、D四点组成的图形是什么图形？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网