Question

14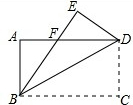．如图，将长方形ABCD沿对角线BD翻折，点C落在点E的位置，BE交AD于点F．求证：重叠部分（即△BDF）是等腰三角形．

Answer 1

分析 由矩形的性质和折叠的性质证出∠ADB=∠EBD，得出BF=DF即可．

解答 证明：∵四边形ABCD是矩形
∴AD∥BC．
∴∠ADB=∠CBD，
由折叠的性质得：∠EBD=∠CBD，
∴∠ADB=∠EBD，
∴BF=DF，
∴△BDF是等腰三角形．

点评 本题考查了矩形的性质、折叠的性质、等腰三角形的判定；熟练掌握矩形的性质和折叠的性质，证出∠ADB=∠EBD是解决问题的关键．