题目内容
2. 如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF是∠AOD的平分线.
如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF是∠AOD的平分线.(1)若∠BOD=60°,求∠DOF的度数;
(2)OE与OF有怎样的位置关系?为什么?
分析 (1)根据角平分线的定义计算即可求出∠BOE,然后根据补角的和等于180°列式计算即可求出∠AOE,先求出∠AOD,再根据角平分线的定义解答;
(2)利用角平分线的定义和平角的定义,可计算出∠EOF的度数.
解答 解:( )∵OE是∠BOD的平分线,∠BOD=60°,
∴∠BOE=$\frac{1}{2}$∠BOD=30°,
∴∠AOE=180°-30°=150°,
∵∠BOD=60°,
∴∠AOD=180°-60°=120°,
∵OF是∠AOD的平分线,
∴∠DOF=$\frac{1}{2}$×120°=60°;
(3)OE⊥OF,
理由:∵OE、OF分别是∠BOD、∠AOD的平分线,
∴∠DOE=$\frac{1}{2}$∠BOD,∠DOF=$\frac{1}{2}$∠AOD,
∵∠BOD+∠AOD=180°,
∴∠EOF=∠DOE+∠DOF=$\frac{1}{2}$(∠BOD+∠AOD)=90°,
∴OE⊥OF.
点评 本题考查余角与补角,角平分线的定义,角度的计算,是基础题,熟记性质并准确识图,找出图中各角之间的关系是解题的关键.

练习册系列答案
相关题目
17.在数-2.5,5$\frac{1}{2}$,0,$\frac{π}{2}$,-1.121121112…,-0.0$\stackrel{•}{5}$中,无理数的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
7.方程x2-3x=0根是( )
| A. | x=-3 | B. | x1=0,x2=-3 | C. | x=3 | D. | x1=0,x2=3 |
12.下列运动过程能表示“平移”的是( )
| A. | 高层住宅电梯的上下运动 | B. | 电风扇叶片的转动 | ||
| C. | 钟表上时针的运动 | D. | 地面上沿直线滚动的足球 |
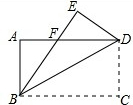 如图,将长方形ABCD沿对角线BD翻折,点C落在点E的位置,BE交AD于点F.求证:重叠部分(即△BDF)是等腰三角形.
如图,将长方形ABCD沿对角线BD翻折,点C落在点E的位置,BE交AD于点F.求证:重叠部分(即△BDF)是等腰三角形.