题目内容
10.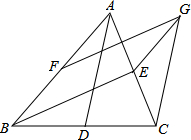 如图,在△ABC中,D、E、F为其三边中点.EG∥AB,FG∥BE,EG与FG交于点G,连接CG,求证:CG=AD.
如图,在△ABC中,D、E、F为其三边中点.EG∥AB,FG∥BE,EG与FG交于点G,连接CG,求证:CG=AD.
分析 可先证明四边形BEGF是平行四边形,可得EG=DE,结合条件可证明四边形ADCG为平行四边形,可得AD=CG.
解答 证明:∵D、E、F分别为BC、AC、AB中点,
∴DE∥AB且DE=BF=$\frac{1}{2}$AB,
∴EG∥BF,
又∵BE∥FG,
∴四边形BEGF是平行四边形,
∴BF=EG=$\frac{1}{2}$AB,
∴EG=DE,
又∵AE=CE,
∴四边形ADCG是平行四边形,
∴AD=CG.
点评 本题主要考查平行四边形的判定和性质及三角形中位线定理的应用,由条件证得DG=DE,利用对角线互相平分证明四边形ADCG是平行四边形是解题的关键.

练习册系列答案
相关题目
20.某商品标价100元,为了促销,商家降价20%后再打9折出售,结果仍盈利20%,则该商品进价是( )
| A. | 60 | B. | 57.6 | C. | 15 | D. | 14.4 |
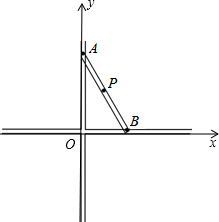 著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能分别在纵向滑槽内、横向滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.按如图所示建立平面直角坐标系.已知AB=10cm,
著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能分别在纵向滑槽内、横向滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.按如图所示建立平面直角坐标系.已知AB=10cm,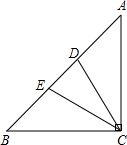 如图,在△ABC中,∠ACB=90°,∠A=45°,AC=AE,BC=BD.求证:△CDE是等腰三角形.
如图,在△ABC中,∠ACB=90°,∠A=45°,AC=AE,BC=BD.求证:△CDE是等腰三角形. 如图,已知?ABCD中,E,F分别是AB,AD上的点,且BF=DE,BF与DE相交于点P,求证:PC平分∠BPD.
如图,已知?ABCD中,E,F分别是AB,AD上的点,且BF=DE,BF与DE相交于点P,求证:PC平分∠BPD.