题目内容
11.一个无盖的纸盒底面积为100cm2的正方形,高为15cm.小丽将一根小木棍斜放在纸盒内,量得露在纸盒外面的部分长是2cm,求出小木棒的总长度.分析 根据正方形的面积公式求得正方形的边长,再进一步求得正方形的对角线的平方,根据勾股定理进而求得纸盒内部的木棒长,从而求得木棒的总长.
解答 解:根据正方形的面积公式,得底面正方形的边长是10cm,则其对角线的平方是100+100=200.
根据勾股定理进一步求得纸盒内部的木棒的长度是$\sqrt{200+225}$=$\sqrt{425}$=5$\sqrt{17}$,
则木棒的总长度是:(5$\sqrt{17}$+2)cm.
点评 此题主要考查了勾股定理的应用,关键是将木棍在长方体中摆放的位置弄清楚,然后运用数学思想进行解题.

练习册系列答案
相关题目
3.已知$\frac{1}{x}$-$\frac{1}{y}$=3,则$\frac{2y+xy-2x}{x-y-xy}$的值为( )
| A. | -$\frac{7}{4}$ | B. | $\frac{7}{4}$ | C. | $\frac{4}{7}$ | D. | -$\frac{4}{7}$ |
4.已知x在数轴上对应的数在0和-1之间,则x2,-x,$\frac{1}{x}$,x对应的各数中,离原数最远的是( )
| A. | x2 | B. | -x | C. | $\frac{1}{x}$ | D. | x |
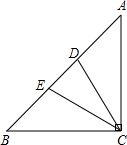 如图,在△ABC中,∠ACB=90°,∠A=45°,AC=AE,BC=BD.求证:△CDE是等腰三角形.
如图,在△ABC中,∠ACB=90°,∠A=45°,AC=AE,BC=BD.求证:△CDE是等腰三角形. 如图,已知?ABCD中,E,F分别是AB,AD上的点,且BF=DE,BF与DE相交于点P,求证:PC平分∠BPD.
如图,已知?ABCD中,E,F分别是AB,AD上的点,且BF=DE,BF与DE相交于点P,求证:PC平分∠BPD.