题目内容
11. 已知正方形ABCD的边长为1,AC为对角线,作DO1⊥AC,O1为垂足,作O1O2⊥AD,O2为垂足,作O2O3⊥AO1,O3为垂足,作O3O4⊥O1O2,O4为垂足,…,请你仔细观察图,然后计算:$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…=1.
已知正方形ABCD的边长为1,AC为对角线,作DO1⊥AC,O1为垂足,作O1O2⊥AD,O2为垂足,作O2O3⊥AO1,O3为垂足,作O3O4⊥O1O2,O4为垂足,…,请你仔细观察图,然后计算:$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…=1.
分析 将算式中的每个加数用对应的三角形的面积来表示,根据图形得到代数式的值等于正方形的面积减去△O1O3O4的面积求解即可.
解答 解:△ABC的面积=△ADC的面积=$\frac{1}{2}$,则$\frac{1}{2}$=1-$\frac{1}{2}$△CDO1的面积=△ADO1的面积=$\frac{1}{{2}^{2}}$;
△AO1O2的面积=△DO1O2的面积=$\frac{1}{{2}^{3}}$,则$\frac{1}{2}$+$\frac{1}{{2}^{2}}$=1-$\frac{1}{{2}^{2}}$;
△O2O3O4的面积=△O1O2O3的面积=$\frac{1}{{2}^{4}}$,则$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$=1-$\frac{1}{{2}^{3}}$;
…
原式=正方形的面积-$\frac{1}{{2}^{n}}$.
当n取无穷大时,$\frac{1}{{2}^{n}}$的值为0.
∴代数式的值=1-0=1.
故答案为:1.
点评 本题主要考查的是正方形的性质,明确代数式的值=正方形的面积-$\frac{1}{{2}^{n}}$是解题的关键.

练习册系列答案
相关题目
6. 如图,AB是圆O的直径,∠ABC=30°,OA=2,则AC的长为( )
如图,AB是圆O的直径,∠ABC=30°,OA=2,则AC的长为( )
 如图,AB是圆O的直径,∠ABC=30°,OA=2,则AC的长为( )
如图,AB是圆O的直径,∠ABC=30°,OA=2,则AC的长为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
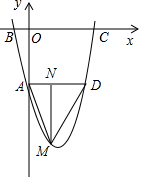 如图,已知二次函数y=ax2+bx+c的图象的顶点坐标为(2,-9),该函数的图象与y轴交于点A(0,-5),与x轴交于点B,C
如图,已知二次函数y=ax2+bx+c的图象的顶点坐标为(2,-9),该函数的图象与y轴交于点A(0,-5),与x轴交于点B,C