题目内容
3.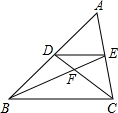 如图,在△ABC中,D、E分别为AB,AC的中点,连接BE,DC交于F点,则△DEF与△BDF的面积比为( )
如图,在△ABC中,D、E分别为AB,AC的中点,连接BE,DC交于F点,则△DEF与△BDF的面积比为( )| A. | 1:2 | B. | 1:4 | C. | 4:9 | D. | 1:3 |
分析 证明DE是△ABC的中位线,由三角形中位线定理得出DE∥BC,DE=$\frac{1}{2}$BC,得出△DEF∽△CBF,得出对应边成比例EF:BF=DE:BC=1:2,得出△DEF与△BDF的面积比=EF:BF,即可得出结果.
解答 解:∵D、E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∴△DEF∽△CBF,
∴EF:BF=DE:BC=1:2,
∴△DEF与△BDF的面积比=EF:BF=1:2;
故选:A.
点评 本题考查了相似三角形的判定与性质、三角形中位线定理、三角形的面积关系;熟练掌握三角形中位线定理,证明三角形相似是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知一个数的倒数的绝对值等于这个数的相反数,则这个数是( )
| A. | 1 | B. | 0 | C. | -1或1 | D. | -1 |
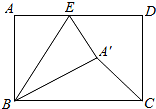 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD 的平分线上时,CA′的长为多少?
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD 的平分线上时,CA′的长为多少?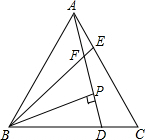 如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.
如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.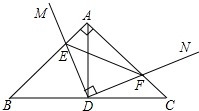 如图,直角△ABC中,∠B=45°,AB=AC=10,点D为BC中点,直角∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.则BE+CF=10.
如图,直角△ABC中,∠B=45°,AB=AC=10,点D为BC中点,直角∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.则BE+CF=10. 如图,将6个相连的正方形分割成8个面积相等的图形,怎么分?画出分割线.
如图,将6个相连的正方形分割成8个面积相等的图形,怎么分?画出分割线.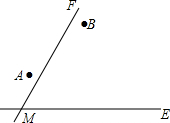 两城镇A、B与两条公路ME、MF位置如图所示,现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
两城镇A、B与两条公路ME、MF位置如图所示,现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部,那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)