题目内容
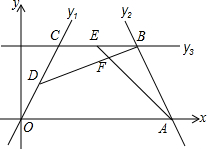 如图在平面直角坐标系中,过点O的直线y1=
如图在平面直角坐标系中,过点O的直线y1=| 3 |
| 3 |
| 3 |
| 7 |
| 2 |
| 3 |
考点:一次函数综合题
专题:
分析:根据C点、B点坐标和D、E分别是线段OC、BC的中点,即可求得直线BD和AE的解析式,即可求得点F的坐标,即可解题.
解答:解:直线y1、y2 分别于y3 交于C、B点,
则C点坐标满足
,解得C点坐标为(
,
)
同理B点坐标为(
,
),
∵点D、E分别是线段OC、BC的中点,
∴D点坐标为(
,
),E点坐标为(7,
)
∴直线BD解析式为y=
x+
,
直线AE解析式为y=-
x+7
,
∵F为AE,BD的交点,
∴F点坐标为(8,3
),
∴BF2=(8-
)2+(
-3
)2=
=
,
∴BF=
.
故答案为
.
则C点坐标满足
|
| 7 |
| 2 |
7
| ||
| 2 |
同理B点坐标为(
| 21 |
| 2 |
7
| ||
| 2 |
∵点D、E分别是线段OC、BC的中点,
∴D点坐标为(
| 7 |
| 4 |
7
| ||
| 4 |
7
| ||
| 2 |
∴直线BD解析式为y=
| ||
| 5 |
7
| ||
| 5 |
直线AE解析式为y=-
| ||
| 2 |
| 3 |
∵F为AE,BD的交点,
∴F点坐标为(8,3
| 3 |
∴BF2=(8-
| 7 |
| 4 |
7
| ||
| 2 |
| 3 |
| 700 |
| 16 |
| 175 |
| 4 |
∴BF=
5
| ||
| 2 |
故答案为
5
| ||
| 2 |
点评:本题考查了平面直角坐标系中,一次函数的运用,本题中求F点坐标是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
Rt△ABC的三边分别为a,b,c,则以下列长度为三边的三角形是直角三角形的是( )
| A、a+1,b+1,c+1 |
| B、a-1,b-1,c-1 |
| C、2a,2b,2c |
| D、a2,b2,c2 |
 如图,已知直线y=(1-k)x+k(k<1)与双曲线y=
如图,已知直线y=(1-k)x+k(k<1)与双曲线y= 如图所示,菱形ABCD的对角线相交于点O,E、F在线段BD上,且BE=DF,判断四边形AECF是不是中心对称图形?如果不是,请说明理由;如果是,求出对称中心.
如图所示,菱形ABCD的对角线相交于点O,E、F在线段BD上,且BE=DF,判断四边形AECF是不是中心对称图形?如果不是,请说明理由;如果是,求出对称中心. 如图,抛物线y=
如图,抛物线y=