题目内容
19. 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为MN(点M、N分别在边AC、BC上),给出以下判断:
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为MN(点M、N分别在边AC、BC上),给出以下判断:①当MN∥AB时,CM=AM;
②当四边形CMDN为矩形时,AC=BC;
③当点D为AB的中点时,△CMN与△ABC相似;
④若AC=3,BC=4,则1≤AD≤3.
其中正确的是①③④(把所有正确的结论的序号都填在横线上).
分析 ①根据平行线的性质得到∠CMN=∠CAB,∠NMD=∠MDA,根据翻折变换的性质得到∠CMN=∠DMN,CM=DM,根据等腰三角形的判定和等量代换证明即可;
②根据折叠的性质得到CM=DE,故四边形CMDN是正方形,根据任意一个直角三角形都有一个内接正方形即可得到结论;
③连接CD,根据直角三角形的性质得到CD=DB=$\frac{1}{2}$AB,于是得到∠DCB=∠B,由轴对称的性质推出∠DCB+∠CNM=90°,由于∠B+∠A=90°,于是得到∠CNM=∠A,即可得到结论;
④分两种情况进行讨论,当N与B重合时,当M与A重合时,分别求得AD的最小值与最大值即可.
解答  解:①∵MN∥AB,
解:①∵MN∥AB,
∴∠CMN=∠CAB,∠NMD=∠MDA,
由翻折变换的性质可知,∠CMN=∠DMN,CM=DM,
∴∠CAB=∠MDA,
∴AM=DM,
∴CM=AM,故①正确;
②根据折叠的性质得到CE=DE,矩形CMDN是正方形,
又∵任意一个直角三角形都有一个内接正方形,故②错误;
③当点D是AB的中点时,△CEF与△ABC相似,
理由如下:如图,连接CD,与MN交于点Q,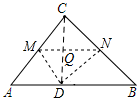
∵CD是Rt△ABC的中线,
∴CD=DB=$\frac{1}{2}$AB,
∴∠DCB=∠B,
由轴对称的性质可知,∠CQN=∠DQN=90°,
∴∠DCB+∠CNM=90°,
∵∠B+∠A=90°,
∴∠CNM=∠A,
又∵∠MCN=∠BCA,
∴△CMN∽△CBA;故③正确;
④若AC=3,BC=4,则Rt△ABC中,AB=5,
如图,当N与B重合时,DB=CB=4,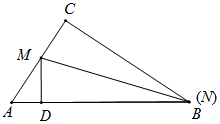
此时,AD=AB-DB=5-4=1;
如图,当M与A重合时,AD=AC=3,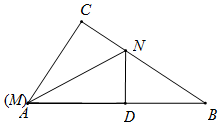
∴1≤AD≤3,故④正确.
故答案为:①③④.
点评 本题主要考查了折叠的性质,勾股定理和相似三角形的判定与性质,掌握翻折变换是一种轴对称,翻折前后对应边和对应角相等,正确运用分类讨论及数形结合思想是解题的关键.

 名校课堂系列答案
名校课堂系列答案 如图,△ABC中,角平分线BO与CO的相交点O,OE∥AB,OF∥AC,BC=10,则△OEF的周长=10.
如图,△ABC中,角平分线BO与CO的相交点O,OE∥AB,OF∥AC,BC=10,则△OEF的周长=10.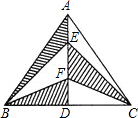 如图,在△ABC中,AB=AC,点D是BC中点,若BC=5,AD=4,则图中阴影部分的面积为5.
如图,在△ABC中,AB=AC,点D是BC中点,若BC=5,AD=4,则图中阴影部分的面积为5.