题目内容
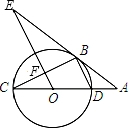 如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.
如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.(1)求证:∠E=∠C;
(2)当⊙O的半径为3,cosA=
| 4 |
| 5 |
考点:切线的性质,勾股定理,平行线分线段成比例
专题:
分析:(1)连接OB,利用已知条件和切线的性质证明:OE∥BD,即可证明:∠E=∠C;
(2)首先求出AB,AO的长,设FB为x,利用勾股定理可得:EB2=EF2+BF2,即62=(2x)2+x2,解方程可求出x的值,进而求出EF的长.
(2)首先求出AB,AO的长,设FB为x,利用勾股定理可得:EB2=EF2+BF2,即62=(2x)2+x2,解方程可求出x的值,进而求出EF的长.
解答:(1)证明:连接OB,
∵CD为⊙O的直径,
∴∠CBD=∠CBO+∠OBD=90°,
∵AE是⊙O的切线,
∴∠ABO=∠ABD+∠OBD=90°,
∴∠ABD=∠CBO,
∵OB、OC是⊙O的半径,
∴OB=OC,
∴∠C=∠CBO,
∵OE∥BD,
∴∠E=∠ABD,
∴∠E=∠C;
(2)解:∵在Rt△OBA中,cosA=
,OB=3,
∴AB=4,AO=5,
∴AD=2.
∴
=
,
∵BD∥OE,
∴
=
,
∴BE=6,
∵OE∥BD,
∴∠EFB=∠CBD=∠OBE=90°,
∵在Rt△OBE中,tanE=
=
=
,
∴在Rt△FBE中,tanE=
=
,
设FB为x,
∵EB2=EF2+BF2
∴62=(2x)2+x2
∴x=
,
∴EF=
.
∵CD为⊙O的直径,
∴∠CBD=∠CBO+∠OBD=90°,
∵AE是⊙O的切线,
∴∠ABO=∠ABD+∠OBD=90°,
∴∠ABD=∠CBO,
∵OB、OC是⊙O的半径,

∴OB=OC,
∴∠C=∠CBO,
∵OE∥BD,
∴∠E=∠ABD,
∴∠E=∠C;
(2)解:∵在Rt△OBA中,cosA=
| 4 |
| 5 |
∴AB=4,AO=5,
∴AD=2.
∴
| AB |
| BE |
| AD |
| OD |
∵BD∥OE,
∴
| 4 |
| BE |
| 2 |
| 3 |
∴BE=6,
∵OE∥BD,
∴∠EFB=∠CBD=∠OBE=90°,
∵在Rt△OBE中,tanE=
| OB |
| BE |
| 3 |
| 6 |
| 1 |
| 2 |
∴在Rt△FBE中,tanE=
| FB |
| FE |
| 1 |
| 2 |
设FB为x,
∵EB2=EF2+BF2
∴62=(2x)2+x2
∴x=
6
| ||
| 5 |
∴EF=
12
| ||
| 5 |
点评:此题考查了切线的判定,圆周角定理,锐角三角函数定义,相似三角形的判定和性质,勾股定理的运用,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目


 平面直角坐标系xOy中,一次函数y=x+n和反比例函数y=-
平面直角坐标系xOy中,一次函数y=x+n和反比例函数y=-
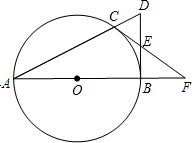 如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.求证:
如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.求证: 样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表: 如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC,请你添加一个条件,使得△ABC和△DEC全等.并加以证明.你添加的条件是
如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC,请你添加一个条件,使得△ABC和△DEC全等.并加以证明.你添加的条件是 已知:AB是⊙O的直径,MN⊥AB,垂足为N,P、Q是
已知:AB是⊙O的直径,MN⊥AB,垂足为N,P、Q是