题目内容

双曲线y₁= $数学公式$ 、y₂= $数学公式$ 在第一象限的图象如图，过y₂上的任意一点A，作x轴的平行线交y₁于B，交y轴于C，过A作x轴的垂线交y₁于D，交x轴于E，连接BD、CE，则 $数学公式$ =________．

$\text{[math]}$
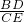分析：由于点A在y= $\text{[math]}$ 的图象上，可设点A的坐标为（a， $\text{[math]}$ ），由于AC⊥y轴，AE⊥x轴，则C点坐标为（0， $\text{[math]}$ ），B点的纵坐标为 $\text{[math]}$ ；E点坐标为（a，0），D点的横坐标为a，而B点、D点在y= $\text{[math]}$ 上，易得B点坐标为（ $\text{[math]}$ ， $\text{[math]}$ ），D点坐标为（a， $\text{[math]}$ ），于是AB=a- $\text{[math]}$ = $\text{[math]}$ ，AC=a，AD= $\text{[math]}$ - $\text{[math]}$ = $\text{[math]}$ ，AE= $\text{[math]}$ ，则AB= $\text{[math]}$ AC，AD= $\text{[math]}$ AE，根据相似三角形的判定易得△BAD∽△CAE，即可得到 $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
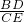解答：设A点的横坐标为a，把x=a代入y= $\text{[math]}$ 得y= $\text{[math]}$ ，则点A的坐标为（a， $\text{[math]}$ ），
∵AC⊥y轴，AE⊥x轴，
∴C点坐标为（0， $\text{[math]}$ ），B点的纵坐标为 $\text{[math]}$ ；E点坐标为（a，0），D点的横坐标为a，
∵B点、D点在y= $\text{[math]}$ 上，
∴当y= $\text{[math]}$ 时，x= $\text{[math]}$ ；当x=a，y= $\text{[math]}$ ，
∴B点坐标为（ $\text{[math]}$ ， $\text{[math]}$ ），D点坐标为（a， $\text{[math]}$ ），
∴AB=a- $\text{[math]}$ = $\text{[math]}$ ，AC=a，AD= $\text{[math]}$ - $\text{[math]}$ = $\text{[math]}$ ，AE= $\text{[math]}$ ，
∴AB= $\text{[math]}$ AC，AD= $\text{[math]}$ AE，
而∠BAD=∠CAD，
∴△BAD∽△CAE，
∴ $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
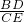故答案为 $\text{[math]}$ ．
点评：本题考查了反比例函数综合题：点在反比例函数图象上，点的横纵坐标满足反比例函数图象的解析式；平行于x轴的直线上的所有点的纵坐标相同；平行于y轴的直线上的所有点的横坐标相同；合理运用相似三角形的判定与性质解决线段之间的比例关系．