题目内容
如图,抛物线y=x²+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
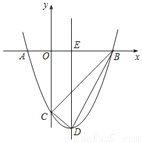
(1)求二次函数解析式及顶点坐标;
(2)点P为线段BD上一点,若S△BCP=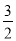 ,求点P的坐标;
,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
(1)y=x ²2x﹣3,D(1, 4);(2)P(2,-2)(3)点M的坐标(5,12)或(, ). 【解析】【解析】 (1)把A(1,0)和B(3,0)两点代入抛物线y=x ²+bx+c中得: ,解得: , ∴抛物线的解析式为:y=x ²2x﹣3=(x1)²4, ∴D(1, 4),………………4分 (2)C(0, 3),由勾股定理得:BC ²=3 ²+3 ²=1...
练习册系列答案
相关题目


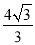 B. 4 C.
B. 4 C. 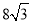 D.
D. 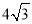
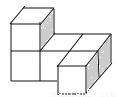
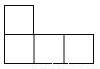 B.
B. 
 D.
D. 
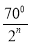 B.
B. 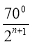 C.
C. 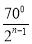 D.
D. 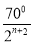
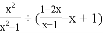 ,其中x满足x2+7x=0.
,其中x满足x2+7x=0.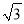 ≈1.73)
≈1.73)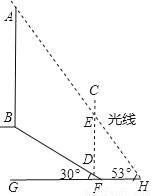
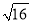 的平方根之和是______.
的平方根之和是______.