题目内容
1．等腰△ABC的腰长AB=10cm，底BC为16cm，则BC边上的高为6cm，△ABC的面积为48cm2．分析 根据等腰三角形的三线合一得BD=8，再根据勾股定理即可求出AD的长，进而求出三角形面积即可．
解答 
解：如图所示：
∵△ABC是等腰三角形，
∴BD=CD=$\frac{1}{2}$BC=8cm，
在Rt△ABD中，则底边上的高为：AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=6cm，
故△ABC的面积为：$\frac{1}{2}$×AD×BC=$\frac{1}{2}$×6×16=48cm2．
故答案为：6cm，48cm2．
点评 本题考查了勾股定理及等腰三角形的性质，解答本题的关键是掌握等腰三角形的三线合一及勾股定理在直角三角形中的表达式．
练习册系列答案
相关题目
11．若分式方程$\frac{x-1}{x-2}$+$\frac{m}{2-x}$=3无解，则m的值为（ ）
| A． | -1 | B． | 1 | C． | -2 | D． | 2 |
16．某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送1035张照片，如果全班有x名同学，根据题意，列出方程为（ ）
| A． | x（x+1）=1035 | B． | x（x-1）=1035 | C． | $\frac{1}{2}$x（x+1）=1035 | D． | $\frac{1}{2}$x（x-1）=1035 |
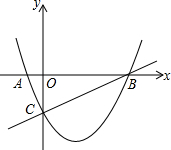如图，已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点，并与直线y=x-2交于B、C两点，其中点C是直线y=$\frac{1}{2}$x-2与y轴的交点，连接AC．
13．若x＞y，则下列式子错误的是（ ）
| A． | x-1＞y-1 | B． | $\frac{x}{3}$＞$\frac{y}{3}$ | C． | x+1＞y+1 | D． | -3x＞-3y |