题目内容
夜晚,小明在路灯下散步.已知小明身高1.5m,路灯的灯柱高均为4.5m.
(1)如图①,若小明在相距10m的两路灯AB,CD之问行走(不含两端),他前后的两个影子长分别为FM=x(m),FN=y(m).试求y与x之间的函数关系式,并指出自变量x的取值范围;
(2)有一个成语叫“形影不离”,其原意为:人的影子与自己紧密相伴,无法分离.但在灯光下,人的速度与影子的速度却不是一样的!如图②,若小明在灯柱PQ前,朝着影子的方向(如图中箭头),以0.8m/s的速度匀速行走,试求他影子的顶端R在地面上移动的速度.
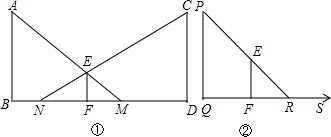
(1)如图①,若小明在相距10m的两路灯AB,CD之问行走(不含两端),他前后的两个影子长分别为FM=x(m),FN=y(m).试求y与x之间的函数关系式,并指出自变量x的取值范围;
(2)有一个成语叫“形影不离”,其原意为:人的影子与自己紧密相伴,无法分离.但在灯光下,人的速度与影子的速度却不是一样的!如图②,若小明在灯柱PQ前,朝着影子的方向(如图中箭头),以0.8m/s的速度匀速行走,试求他影子的顶端R在地面上移动的速度.

考点:相似三角形的应用,中心投影
专题:
分析:(1)易证△MEF∽△MAB,根据相似三角形的对应边的比相等.可以把BF用x表示出来,同理,DF也可以用y表示出来.根据BD=10,就可以得到x,y的一个关系式,从而求出函数的解析式.
(2)根据△REF∽△RPQ就可以求出PE与RP的比值,同理.根据△PEE′∽△PRR′,求得EE′与RR′的比值.则影子的速度就可以得到.
(2)根据△REF∽△RPQ就可以求出PE与RP的比值,同理.根据△PEE′∽△PRR′,求得EE′与RR′的比值.则影子的速度就可以得到.
解答: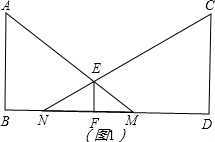 解:(1)∵EF∥AB,
解:(1)∵EF∥AB,
∴∠MEF=∠A,∠MFE=∠B.
∴△MEF∽△MAB.
∴
=
=
=
.
∴
=
,MB=3x BF=3x-x=2x.
同理,DF=2y.
∵BD=10
∴2x+2y=10
∴y=-x+5
∵当EF接近AB时,影长FM接近0;
当EF接近CD时,影长FM接近5
∴0<x<5;
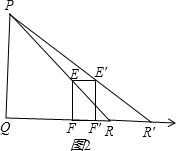 (2)如图,设运动时间为t秒,则EE'=FF'=0.8t
(2)如图,设运动时间为t秒,则EE'=FF'=0.8t
∵EF∥PQ
∴∠REF=∠RPQ,∠RFE=∠RQP
∴△REF∽△RPQ
∴
=
=
=
,
∴
=
,
∵EE'∥RR'
∴∠PEE'=∠PRR',∠PE'E=∠PR'R
∴△PEE'∽△PRR'
∴
=
,
∴
=
,
∴RR'=1.2t,
∴V影子=
=1.2米/秒.
 解:(1)∵EF∥AB,
解:(1)∵EF∥AB,∴∠MEF=∠A,∠MFE=∠B.
∴△MEF∽△MAB.
∴
| MF |
| MB |
| EF |
| AB |
| 1.5 |
| 4.5 |
| 1 |
| 3 |
∴
| x |
| MB |
| 1 |
| 3 |
同理,DF=2y.
∵BD=10
∴2x+2y=10
∴y=-x+5
∵当EF接近AB时,影长FM接近0;
当EF接近CD时,影长FM接近5
∴0<x<5;
 (2)如图,设运动时间为t秒,则EE'=FF'=0.8t
(2)如图,设运动时间为t秒,则EE'=FF'=0.8t∵EF∥PQ
∴∠REF=∠RPQ,∠RFE=∠RQP
∴△REF∽△RPQ
∴
| RE |
| RP |
| EF |
| PQ |
| 1.5 |
| 4.5 |
| 1 |
| 3 |
∴
| PE |
| RP |
| 2 |
| 3 |
∵EE'∥RR'
∴∠PEE'=∠PRR',∠PE'E=∠PR'R
∴△PEE'∽△PRR'
∴
| EE′ |
| RR′ |
| PE |
| RP |
∴
| 0.8t |
| RR′ |
| 2 |
| 3 |
∴RR'=1.2t,
∴V影子=
| 1.2t |
| t |
点评:考查相似三角形的应用;用到的知识点为:平行于三角形一边的直线与三角形另两边相交,截得的两三角形相似;相似三角形的对应边成比例.

练习册系列答案
相关题目
2012年4月13日国家统计局举行发布会,一季度全国城镇新增工作岗位332万个,332万个可用科学记数法表示为( )
| A、3.32×105个 |
| B、3.32×106个 |
| C、33.2×105个 |
| D、0.332×107个 |
一次函数y=7x-3的图象不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
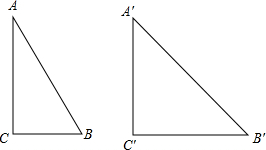 如图,在△ABC中,∠C=90°,∠A=30°.在△A′B′C′中,∠C′=90°,A′C′=B′C′.能否分别将这两个三角形各自分割成两个三角形,使△ABC所分成的两个三角形与△A′B′C′所分成的两个三角形分别对应相似?若能,请设计一种分割方案;若不能,请说明理由.
如图,在△ABC中,∠C=90°,∠A=30°.在△A′B′C′中,∠C′=90°,A′C′=B′C′.能否分别将这两个三角形各自分割成两个三角形,使△ABC所分成的两个三角形与△A′B′C′所分成的两个三角形分别对应相似?若能,请设计一种分割方案;若不能,请说明理由.
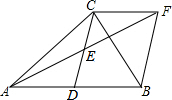 如图,在△ABC中,D是AB的中点,E是CD的中点,延长AE到F点,使得E是AF的中点,连接BF,CF.求证:DC=BF.
如图,在△ABC中,D是AB的中点,E是CD的中点,延长AE到F点,使得E是AF的中点,连接BF,CF.求证:DC=BF. 如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:
如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证: