题目内容
2.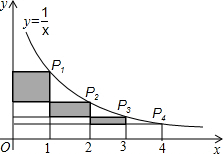 在反比例函数y=$\frac{1}{x}$(x>0)的图象上,有点P1,P2,…,P2011,…,它们的横坐标依次为1,2,…2011,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,…,S2010…,则S1+S2+…+S2010=$\frac{2010}{2011}$.
在反比例函数y=$\frac{1}{x}$(x>0)的图象上,有点P1,P2,…,P2011,…,它们的横坐标依次为1,2,…2011,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,…,S2010…,则S1+S2+…+S2010=$\frac{2010}{2011}$.
分析 根据反比例函数的几何意义可知图中所构成的阴影部分的面积和正好是从点P1向x轴,y轴引垂线构成的长方形面积减去最下方的长方形的面积.
解答  解:由题意可知点P1、P2、P3,…,P2010纵坐标分别为:1,$\frac{1}{2}$…$\frac{1}{2010}$,
解:由题意可知点P1、P2、P3,…,P2010纵坐标分别为:1,$\frac{1}{2}$…$\frac{1}{2010}$,
由反比例函数的几何意义可知:
S1+S2+…+S2010=${S}_{四边形{DP}_{1}BO}$-S四边形ABCO=1-$\frac{1}{2011}$=$\frac{2010}{2011}$.
故答案为:$\frac{2010}{2011}$.
点评 此题主要考查了反比例函数的综合应用,根据已知得出长方形面积减去最下方的长方形的面积是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在Rt△ABC中,∠C=90°,若sinA=$\frac{2}{3}$,则tanB=( )
| A. | $\frac{5}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
10.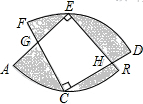 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点.若扇形的半径是2,则图中阴影部分的面积等于( )
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点.若扇形的半径是2,则图中阴影部分的面积等于( )
 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点.若扇形的半径是2,则图中阴影部分的面积等于( )
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点.若扇形的半径是2,则图中阴影部分的面积等于( )| A. | 2π-4 | B. | 2π-2 | C. | π+4 | D. | π-1 |
12.下列运算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | a8÷a4=a2 | C. | 3$\sqrt{2}-\sqrt{2}$=3 | D. | a2•a3=a5 |
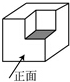 如图的几何体是由一个正方体切去一个小正方体形成的,它的左视图是( )
如图的几何体是由一个正方体切去一个小正方体形成的,它的左视图是( )