题目内容
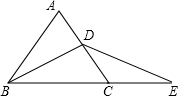 如图,在等边△ABC中,BD平分∠ABC,延长BC到点E,使CE=CD,连接DE.
如图,在等边△ABC中,BD平分∠ABC,延长BC到点E,使CE=CD,连接DE.(1)BD与DE有什么关系?试说明理由;
(2)把BD改成什么条件,还能得到同样的结论.
考点:等边三角形的性质,等腰三角形的性质
专题:
分析:(1)首先由在等边△ABC中,D是AC边中点,根据三线合一与等边对等角的性质,即可求得∠ABC=∠ACB,∠DBC=
∠ABC,又由CE=CD,根据等边对等角的性质,可得∠E=∠CDE,又由三角形外角的性质,即可求得∠E=
∠ACB,则可得∠E=∠DBC,然后利用等角对等边,即可证得BD=DE.
(2)根据等边三角形三线合一的性质即可更改BD的条件.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据等边三角形三线合一的性质即可更改BD的条件.
解答:解:BD=DE.
理由:∵在等边△ABC中,D是AC边中点,
∴∠ABC=∠ACB=60°,∠DBC=
∠ABC=30°,
∵CE=CD,
∴∠E=∠CDE,
∵∠ACB=∠E+∠CDE,
∴∠E=
∠ACB=30°,
∴∠E=∠DBC,
∴DB=DE.
(2)把BD改成BD⊥AC或BD平分AC,还能得到同样的结论.
理由:∵在等边△ABC中,D是AC边中点,
∴∠ABC=∠ACB=60°,∠DBC=
| 1 |
| 2 |
∵CE=CD,
∴∠E=∠CDE,
∵∠ACB=∠E+∠CDE,
∴∠E=
| 1 |
| 2 |
∴∠E=∠DBC,
∴DB=DE.
(2)把BD改成BD⊥AC或BD平分AC,还能得到同样的结论.
点评:本题考查了等边三角形各边相等的性质,等腰三角形底角相等的性质,本题中求证∠CBD=∠CED是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
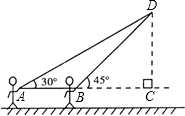 放风筝是广受喜爱的一种运动,星期天的上午小明在大运河广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树捎上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°.为了便于观察,小明迅速向前边移动边收线到达了B处,此时风筝BD与水平线的夹角为45°.已知点A、B、C在同一条直线上,∠ACD=90°,点B距大树CD的水平距离为8米.请你求出小明此时所收回的风筝线的长度是多少米?(结果保留根号)
放风筝是广受喜爱的一种运动,星期天的上午小明在大运河广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树捎上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°.为了便于观察,小明迅速向前边移动边收线到达了B处,此时风筝BD与水平线的夹角为45°.已知点A、B、C在同一条直线上,∠ACD=90°,点B距大树CD的水平距离为8米.请你求出小明此时所收回的风筝线的长度是多少米?(结果保留根号) 如图,这是某小区绿化带的平面示意图(单位m)
如图,这是某小区绿化带的平面示意图(单位m) 如图,在直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△ABO,点C为x轴正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.下列结论正确的有( )个:
如图,在直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△ABO,点C为x轴正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.下列结论正确的有( )个: